Wondering how to explain and simplify radicals with variables? Read on to discover strategies for making this task easier.
#1 – Review Concepts Related to Radicals
Preparation for simplifying variables in radicals is best accomplished by reviewing terms related to radicals. This provides a foundation for understanding concepts related to simplifying variables. It also makes it easier for students to formulate questions, using accurate terminology.
Students will also benefit from a review of expanding numbers and variables with exponents, and rules for exponents when multiplying variables.
Below, key terms are color-coded.
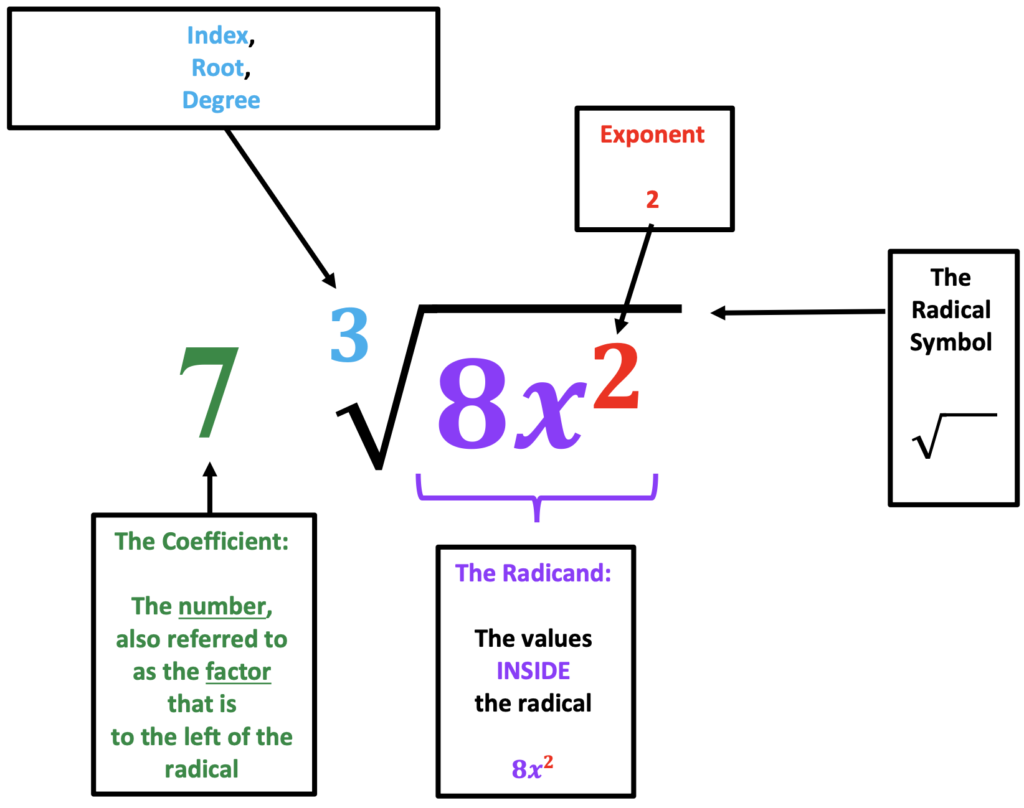
Below is an example to “read” and identify color-coded terms.
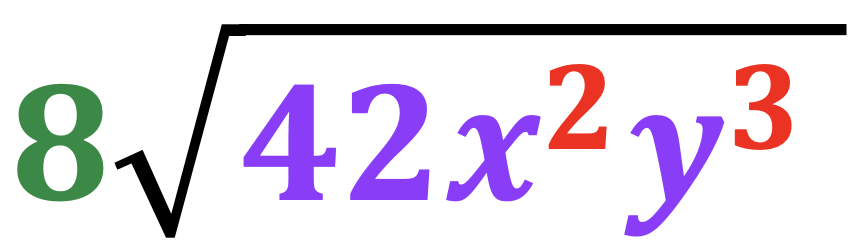


#2 – Single Variables of Radicals: Simplified
Next, provide students with examples representing radicals in simple terms. Provide examples of radicals with different indices.
Notice that when the index and exponent value are the same, the radical simplifies to a variable in simplest form. In each of these examples, the coefficient is x.
(The exponent of one has been left on the variable to help emphasize the exponent value).
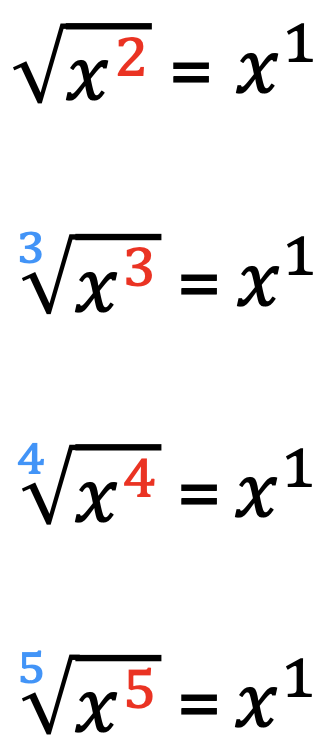
**************************************************************************************************************************************************************************
#3 – Simplifying Radicals with Variables
After emphasizing characteristics of radicals that simplify when the index and exponent are the same value, proceed to simplify variables with various exponent values. Use colorful examples. Present in a question/answer format as illustrated in the example below.







Observe the progression for simplifying variables in the following examples.
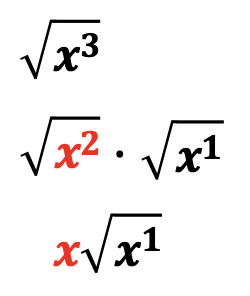
A radical with an index of five can only be simplified if the variable inside the radical sign has a variable with an exponent of five or greater. In the example below, notice that the exponent value for x is less than five. This means that the radical is not able to be simplified.

The example below represents three variables, x, y, and z. In this problem, all variables have been factored. The factors in red, green, and blue can be simplified. The remaining variables with exponents less than two will remain under the radical sign.
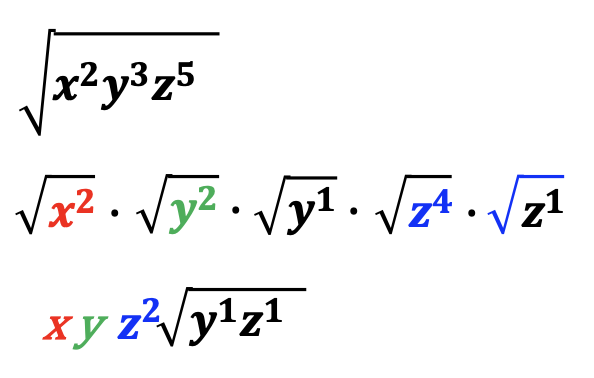
Similarly, red, green, and blue factors can be simplified. In the final answer, y and z squared will remain inside the radical sign as the exponents of these variables are less than three.
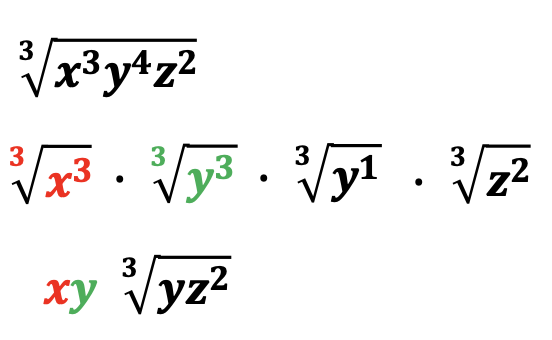
Furthermore, a radical with an index of five will result similarly.
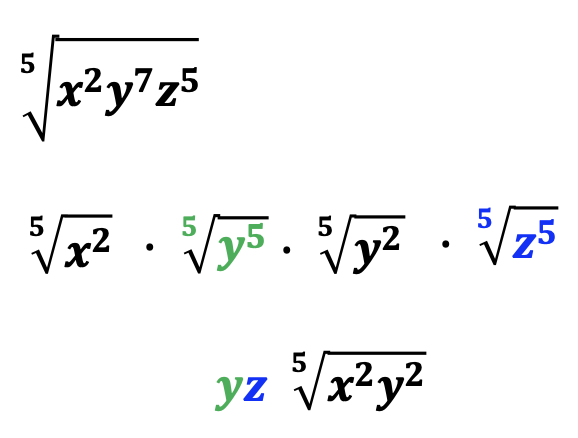
#4 – Simplifying Radicals with Numbers and Variables
Finally, for the grand finale! When radicals include numbers and variables, the rules remain the same.
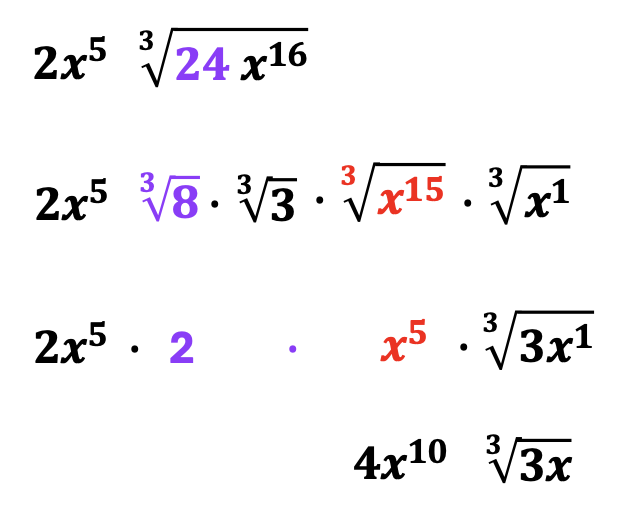
Conclusion
You now have strategies for helping students learn how to simplify radicals with variables. Remember, prepare students by reviewing previous concepts and providing several examples in a question/answer format with accents of color!
You may also enjoy reading the following related posts.
Just click on any of the titles below.
Looking for More Materials?
Click the button below to view more of my educational resources!
