How to Create a Fibonacci Sequence Problem Solving Puzzle
Looking for engaging activities to spice up math topics on number patterns and special sequences of numbers? In this post, you will be introduced to the Fibonacci sequence and other craft ideas including detailed directions for creating a Fibonacci puzzle.
#1 – Introduction to the Fibonacci Sequence
I welcome you to the wonderful adventure of a significant number pattern!
The Fibonacci sequence is a special number pattern. An example of these numbers in sequential order is as follows:
0, 1, 1, 2, 3, 5, 8, 13, and 21, and continuing into infinity, repeating a specific pattern.
When I introduce the first few Fibonacci numbers to my students, I love to list the sequence of numbers on the board and ask if they can find a pattern or expression that may be used to continue the pattern. To increase student involvement, I encourage students may work together in small groups of two to three.
As students work together, they will discover the next number by adding the two numbers before it. For example, see the illustration below:


Following student discovery, I share that these numbers are found in nature, such as petals on a flower, and spirals found in sunflowers and roses. It is at this time that I will share the following fun video:
Doodling in Math: Spirals, Fibonacci, and Being a Plant [1 of 3]
https://www.youtube.com/watch?v=ahXIMUkSXX0



#2 – Supplies to Make the Puzzle
40 wooden craft blocks per puzzle
The size of the wood blocks may be as small as 1/4 an inch or larger. A larger block will require more time to paint, though may be easier for students to hold.
8 colors of craft paint (Glossy acrylic is my favorite, though it does not wash out well.)
Paint smocks for students to keep clothes from paint spills
Lightgrade sandpaper
Dusting cloth
Paint brushes to fit the size of the block
Re-cycled plastic containers to fill with rinse water and to soak brushes
Plastic covering to place over the craft table
Flexible material that can be formed into a spiral: shoe lace, yarn, pipe-cleaner or other bendable material.
Below is a picture of the completed Fibonacci puzzle.
The numbers in black represent the number sequence: 1, 1, 2, 3, and 5.
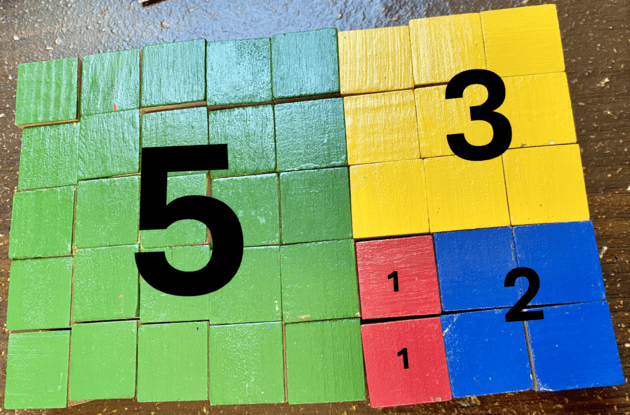
Other materials that may be used to complete a similar project: craft foam sheets (as shown below), construction paper, felt, quilting squares, crochet granny squares, and other similar materials.

#3 – Directions
After all materials have been laid out, read and demonstrate the directions for completing the project.
Step 1:
Sketch and color in your design on graph paper. See the video below for instructions for sketching your puzzle.
How to Draw a Fibonacci Spiral with Graph Paper
https://www.youtube.com/watch?v=sD51wFfIrfIhis is point number 3.
The puzzle shown in this post is 5 x 8., a total of 40 blocks.
Step 2:
To increase the challenge of the puzzle, design another puzzle, the same dimensions, with different colors that will be painted on the opposite side of the block.
Step 3:
Gently sand each block, smoothing out any jagged edges. Next, wipe each block with a dusting cloth to remove any sawdust. This will create a smoother painting surface.
Step 4:
Prepare to paint. Put on smock to protect clothing. Pick out a paint brush and paint colors.
Step 5:
Refer to your sketches for your Fibonacci puzzle.
Suggestion:
There are two sides of the block that tend to have a rougher surface. Paint on the smoothest side. The smoother sides will give the painted block a smoother look after it is painted.
Begin by painting your first sketch, using chosen colors.
Step 6:
Next, allow the paint to dry for at least 24 hours in a well ventilated area.
Step 7:
When the paint is completely dry, begin painting the opposite side of each block, using your second sketch and chosen colors.
Step 8:
Again, allow the paint to dry for at least 24 hours in a well ventilated area.
Step 9:
Create a spiral shape that can be placed over the completed Fibonacci puzzle.
Step 10:
Mix up the puzzle blocks. Set a timer to see how long it takes to put the puzzle back together. Next, share it with a friend. If the friend is not familiar with the Fibonacci pattern, provide hints as needed.
In addition, consider variations to the directions listed above.
Variations:
1. Sketch and color-code the puzzle so that the design will be the same on both sides. For example, if the puzzle was turned over, the design would be the same. Use different colors on the opposite side of the block to make the puzzle more challenging.
2. Brain storm with a partner to determine other variations for puzzle design that may make the puzzle more complex, though able to solve.
3. Consider other materials that can be recycled to create a similar puzzle.
4. Assessment: On graph paper, students design and number as many consecutive Fibonacci sequences as possible. Some students may need to tape another page of graph paper to the original page. This will provide more space to extend the size of the design.
#4 – Other Craft Ideas
In addition, there are four other craft ideas listed below that you may like to try.
Notice how the paint makes the spirals of the pinecone stand out. Suggestion: Begin painting from the bottom of the pinecone and work up.

I found these flowers and leaves in my front lawn. Clip and leaves and flowers, lay each on flat on paper. Cover with another paper. Place in a book to flatten and dry. Next, remove a flower or leave. Dot the flower or leaf with glue and place it on a strip of construction paper. After the glue has dried, laminate the strip. This craft can be used to create book markers, and cards or to decorate other items.

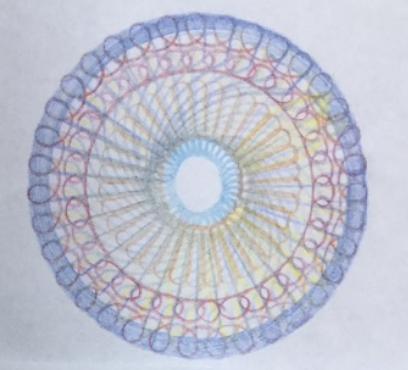
Spirograph Art: Notice the spiral concept in the middle.
String Art: Though more detailed than the puzzle, this craft form may also be created. Notice the graph paper below, used as a guide.

Conclusion
Learning about special number sequences is fascinating and fun at the same time! As students think through designing puzzles and exploring nature, they experience creative and engaging problem-solving opportunities for themselves and others.
Looking for More Materials?
Click the button below to view more of my educational resources!
