Creating a foundation is critical for success with percent word problems. Keep reading to discover the concepts needed to provide this success.

#1 – Review Fraction, Decimal and Percent Conversions
Once you have survived teaching fraction and decimal problems, there is one more hurdle left. The ominous subject of percent. More specifically, how to solve percent word problems.
However, if you have students who continue to struggle with converting between fractions, decimals, and percent, a brief review can save you time in the long run.
A. Converting from Fraction to Decimal, and Percent
First, review converting from fractions to decimals. I always like to use a fraction students are most familiar with, such as 1/4. While explaining the process, students need to write down the example and solve as each step is listed.
In addition, I do not fret about calculators used when dividing such numbers as 1 divided by 4. On the other hand, if I have students who can, I encourage them to do so.
To discover more about fractions, decimals, percent, and rounding click the links below.
Fractions, Decimals, and Percent: How to Prepare Students
How to Convert Between Fractions, Decimals and Percent
In the example below, 1/4 results in a number with the last digit ending in the hundredth place. Other fractions such as 7/8 do not. When this occurs, I recommend that students round the number to the nearest hundredth. Yes. This concept may also need to be reviewed.

Second, practice converting decimals to percent by following the directions and illustrations below.

When students include the invisible decimal, it helps reinforce the concept that the decimal moves two places to the right. After students have placed the invisible zero, students write the number below, without the decimal as described below.
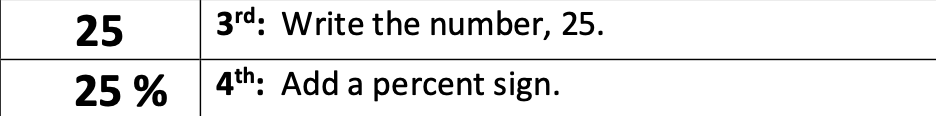
A simplified version of decimal to percent:
1. Move the decimal two places to the right.
2. Drop the decimal.
3. Add a percent sign after the number.
B. Converting from Percent to Decimal
Furthermore, converting from a percent to a decimal is the reverse of converting a decimal to a percent. Though I may say this to students, I find an example is worth doing. See the example below.

C. Converting from a Decimal to a Fraction
Though converting between decimals and percents is usually quickly understood, converting from a decimal to a fraction appears to challenge students the most. Also consider that an understanding of place value is needed with this process, too. Below, steps for converting from decimal to fraction are described from left to right.

When using this example, underline the last digit after the decimal point. Next, write the first letter representing the value of the last digit. In this example, the last digit is five. It is in the hundredths place. Notice that the “h” for hundredths is written below the decimal number. This is done to reinforce the structure of the fraction, in preparation for the next step, writing the fraction.
Next, students write the number, “25” in the numerator and “100” in the denominator. I always write the “TH” in capital letters to remind students of the place value.
Students can now write the numbers representing the words, and “PRESTO!” We have a fraction!
Ooops. It is not reduced yet. Many students will recognize that 25/100 can be reduced to 1/4. For students who do not recognize this, factors of the numbers may be written to select the greatest common factor, which in this case is 25.
#2 – Keywords, Phrases and the Ratio
Once students understand conversions between fractions, decimals and percents, introduce keywords and phrases commonly associated with percent problems. An understanding of the ratio is also important.
A. Keywords and Phrases for Percent Word Problems

B. The Ratio: A Component of Percent Word Problems
Next, give examples of how ratios are used.
Explain that ratios are useful tools for everyday life because they help us compare values. For example, sports scores are written comparing wins to losses. 4 wins to 5 losses. When 4 is divided by 5 the result is 0.8 or 80 %. This means that 80/100 percent of the time, or 80 percent of the time the team has won games. It also means that 20 percent of the time the team has lost. Also, explain the three common forms in which ratios are represented. See below.

Below is another example that illustrates these three forms.

#3 – Putting It All Together
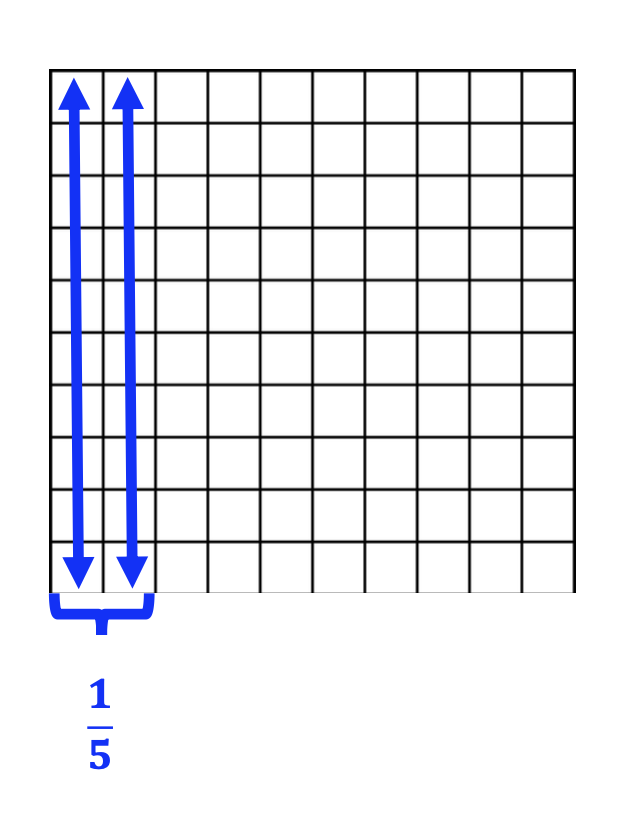
To help students visualize the big picture, use a grid with 100 squares. Using this simple technique, students are able to see connections between fractions, ratios, percent, part and whole.
See below.
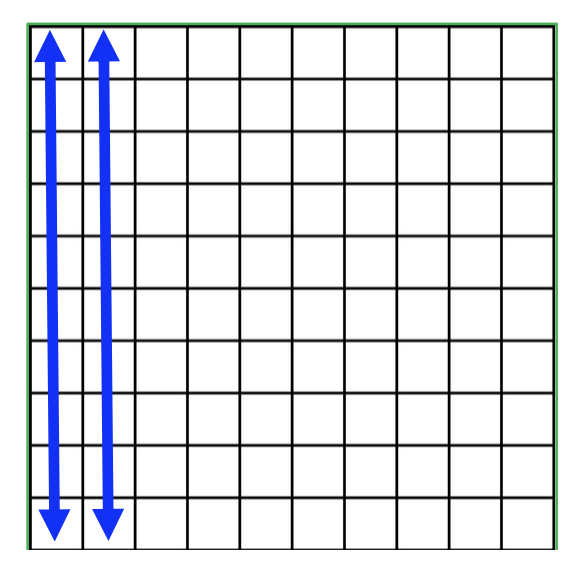


Note that the ratio concept resurfaces, again.


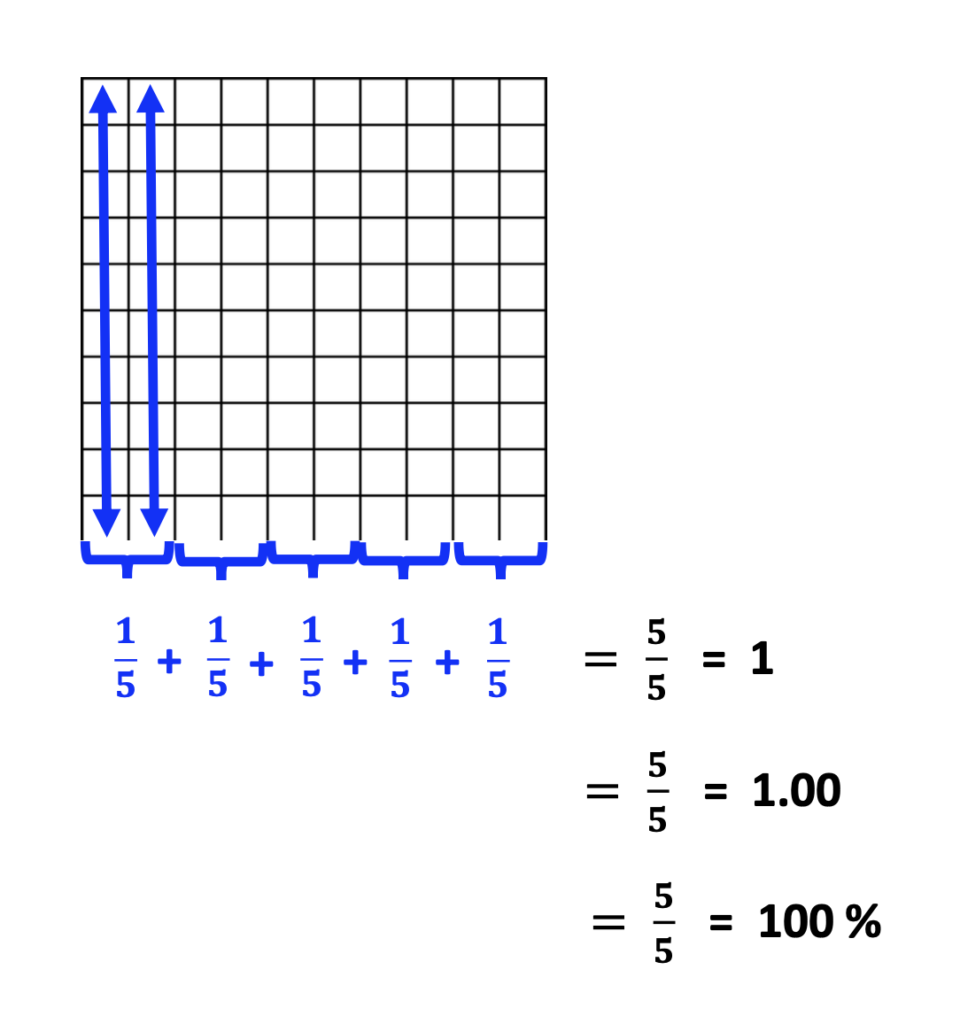
In the above illustration, it is easy to see that when the parts are added together, it results in a whole which can be written as a whole number, 1, as a decimal, 1.00, and 100 %.
Conclusion
Students with a solid understanding of fraction-decimal-percent conversions, keywords, phrases, the ratio, and instruction with visual representation will best prepare students for success with percent word problems.
You can do it!
Looking for More Materials?
Click the button below to view more of my educational resources!
