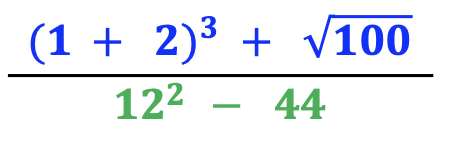Are students ready to solve the order of operations with rational expressions? Do all students understand how to solve all fractions and simplify integers, exponents, and roots? Keep reading to discover how to solve the order of operations with rational expressions.
#1 Prepare by Providing Supports
You have likely observed that the order of operations with rational expressions is a common challenge for students. Before diving into these problems, consider resources that can be provided for those needs. For example, you recognize some students struggle with math tasks such as fraction operations, integers, exponents, roots, and distributive property. There will be other students who have learned how to do these operations, yet will benefit from resources they can refer to when they forget.
To cover this need, provide support resources to students, such as posters, graphic organizers, and cheat sheets. Examples may include:
1. Posters or graphic organizers that explain the steps for solving each type of fraction operation.
2. Posters illustrating the order of operations
3. Cheat Sheets for the integer rules, exponents, and roots.
Next, provide students with a quick review of each topic while pointing out where the source is located. Encourage students to utilize these resources at any time. This will save you time answering questions students can find on their own.
Below you will find a resource that provides posters for fraction operations. Each poster includes illustrations and step-by-step instructions. For more details, click the link below.

#2 Start Small: Order of Operations with Rational Expressions
Now you are ready to begin by providing a simple example that will also introduce students how to solve the problem. See the example below.
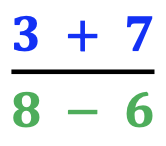
When illustrating an example, emphasize that all of the terms at the top and bottom of the rational expression will be solved separately, one at a time.
Also, note that the terms at the top of the rational function are blue. The terms at the bottom are green. The final answer is in black. The use of color helps students visually organize and make sense of the information.
In addition, point out that the order of operations is solved from left to right. The steps of the problem are also written from left to right. This decreases student confusion by keeping the top terms at the top and the bottom terms at the bottom.
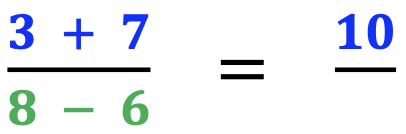
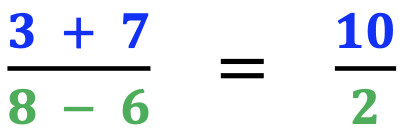
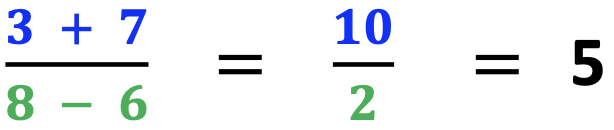
#3 Include Examples with Parentheses
Remind students that the rules for parentheses remain the same as with any other expression. Provide an example such as the one below.
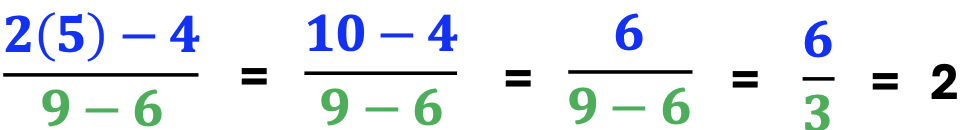
Though the steps have all been written, remind students to start and finish solving the top or bottom of the expression before doing the other. In this example, some students may prefer to solve 9 – 6 and then carry the 3 to the end of the problem.
Before moving on to exponents and roots, example problems using absolute value signs and integers may also be included.
#4 Include Examples with Exponents and Roots
Next, include examples of parentheses, exponents, and roots.
A. Parentheses and Exponents
Next, provide an example with parentheses and exponents. Remind students to continue to follow the rules for the order of operations.
Also, add they may use their cheat sheets for exponents as needed.
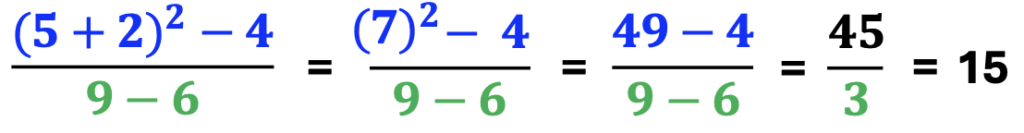
B. Parentheses and Roots
Now provide examples with roots.
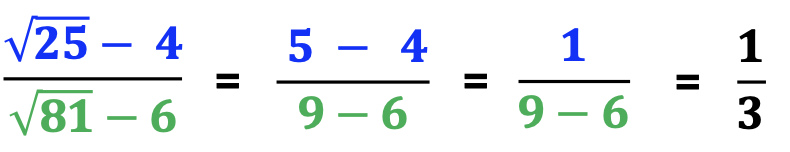
C. Parentheses, Roots, and Exponents
Finally, include examples with parentheses, roots, and exponents such as the example below.
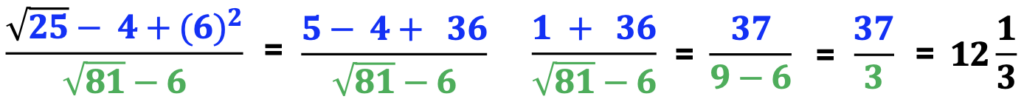
D. Order of Operations with Rational Expressions: Group Activity
After finishing these problems, provide practice opportunities. Provide options.
1. Students completing a worksheet with another peer or in a small group.
2. Students write problems for others in a small group. Next, they take turns solving each other’s problems. If the answers are not all the same, students will re-work the problem until arriving at the same solution.
This activity allows students to talk through what they have learned.
Conclusion
As instruction is provided in a step-by-step, visual way, students will understand how to solve rational expressions. Success with these problems will increase their success in future algebraic rational expressions.
Other Related Posts
Looking for More Materials?
Click the button below to view more of my educational resources!