Domain and range? Algebraic functions? Have you found that your students struggle to understand these concepts in Algebra? Keep reading to discover how to help students understand the vocabulary used with algebraic functions, including domain and range.
#1 Skills to Know Before Domain, Range, and Functions
Are your students prepared to begin algebraic functions?
Domain and range of algebraic functions are best understood after students are confident in the concepts listed below.
How to:
1. Solve operations with variables
2. Simplify expressions
3. Solve linear equations
4. How to solve inequalities
5. Explain the elements of the coordinate plane
x and y axes
Origin
Quadrants
Negative and Positive numbers on the x and y-axis
Slope types: negative (descending line), positive (ascending line), zero slope (horizontal line),
undefined line (vertical line) represented by repeating x values
6. State the equation of a line on a graph
7. Identify the ordered pairs of points on a line.
Students who understand these concepts will have a foundation to understand new information related to a function, domain, and range.
Looking for additional information on the above topics? See the links below:
How to Successfully Introduce the Cartesian Plane
How to Successfully Explain the Relationship Between x/y Coordinates and Linear Equations
#2 – A Tasty Way to Introduce Functions
Are you looking for a great way to get students on board for learning functions?
Provide students with a concrete understanding of functions using a real machine.
Make fruit smoothies!
1. To prepare, you will need a smoothie machine, different kinds of fruit, paper cups, and towels for cleanup.
2. Each different fruit will represent a single x-value, the input.
3. Explain that the machine has certain rules it can follow. It can chop, dice, or puree.
4. The resulting smoothie will represent the y-value, the output.
For example, strawberries will create an output of a strawberry smoothie.
Create another smoothie by choosing a different fruit, and re-emphasizing the words, “input,” machine,” and “output.”

Next, explain that just as a smoothie machine must follow a rule, algebraic functions also follow a specific rule.
Draw a simple illustration on the board. See the example below.
Emphasize that a linear function will result only if one input is placed into the machine at a time, just like only one type of fruit was put into the smoothie machine.
Observe the illustration below.
Note that when an input of -3 is placed into the “machine,” the math “machine” substitutes -3 for the x variable, resulting in an output or y-value, -3.

This process may be repeated with several other input values.
For example, positive 7 could be used as an input value. See below.
Input: 7
Rule: 2x + 3
2(7) + 3
14 + 3
Output = 17
Next, share that as inputs refer to the x value and outputs refer to the y value, two other terms are also used.
DOMAIN: a term used to describe inputs, x values.
RANGE: a term used to describe outputs, y values.
Domain and range are terms that will commonly be used in future functions encountered in Algebra.
#3 – Function, Domain, and Range: The Big Picture
Furthermore, it is important to understand how all these concepts connect.
Below is a list of characteristics used to determine whether a line represents a function. Notice how the x values never repeat.
A. Line on a graph
B. An equation
C. Ordered pairs
D. Table of x and y values
E. Mapping
Observe the illustration below.
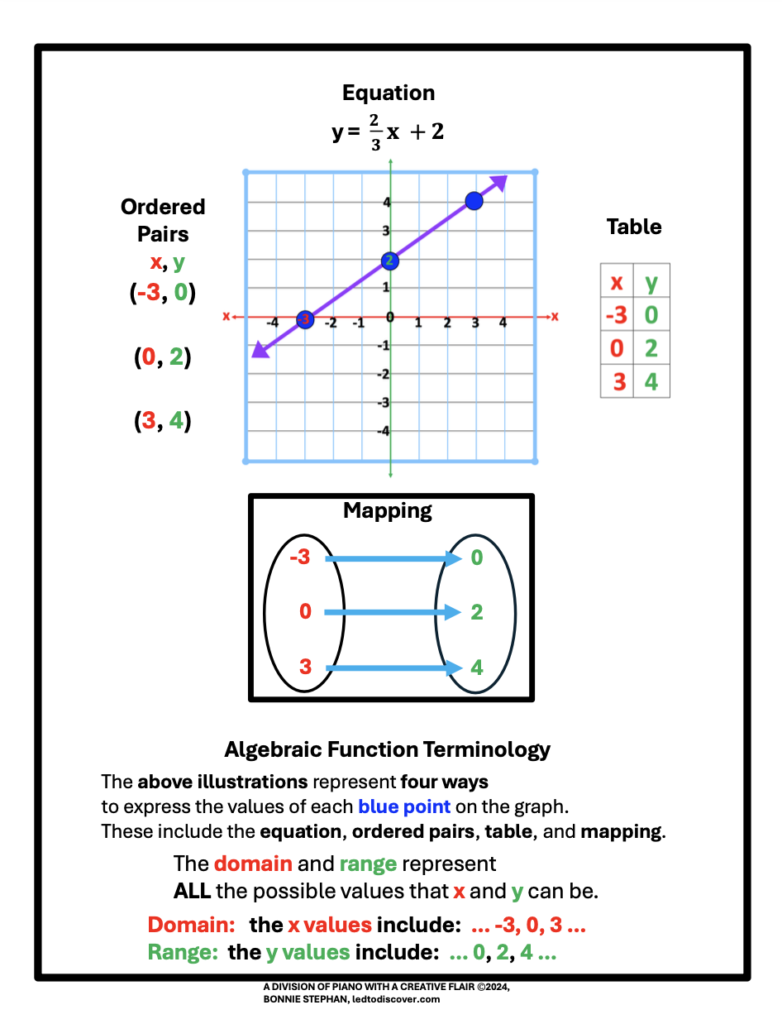
Notice that the x values never repeat. If x values did repeat, this equation would not represent a function.
The domain and range express ALL the possible x and y values represented by the function.
#4 – Domain, Range and Interval Notation
Furthermore, interval notation is in a sense, a shorter version that represents all possible values of the domain and range. Symbols used with interval notation may include parentheses, brackets, numbers, and infinity signs.
For example, the function, y = 2/3 + 2 may be represented by interval notation. See below.

This means that the length of the line will never end.
Conclusion
To summarize:
1. The ability to understand graphing concepts is valuable for understanding functions.
2. A function “machine” illustrates how the input, the rule of the “machine” and the output values operate.
The terms input, x-value, and domain refer to the x-values of a function.
The terms output, y-value, and range refer to the y-values of a function.
3. The x and y values of a linear function may be illustrated in the following ways:
A. Line on a graph
B. An equation
C. Ordered pairs
D. Table of x and y values
E. Mapping
4. Domain and range may be represented using interval notation.
Though this information may be challenging for students, taking a step-by-step approach, and introducing new information, alongside what is known, will help students make connections between these concepts.
You can do this!
Looking for More Materials?
Click the button below to view more of my educational resources!
