Do equations, fractions, and parentheses combined, cause math anxiety for your students? Discover strategies that will help.
#1 – Are Students Ready? Equations, Fractions, and Parentheses
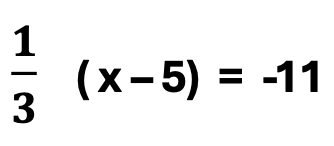
A. Readiness Skills for Equations, Fractions, and Parentheses
Are students ready for equations, fractions, and parentheses all in one problem? Let’s look at student-acquired math skills that increase student success with problems that include equations, fractions, and parentheses. These math skills include the ability to:
- 1. Determine the Least Common Multiple, L.C.M.
2. Complete all fraction operations
3. Demonstrate understanding of integer rules
4. Apply distributive property in expressions and equations
5. Complete two to three step equations
Furthermore, concepts that require the most review include the L.C.M and fraction operations. To help increase student confidence, I provide my students with fraction operation practice from the beginning to the end of the school year. Both middle and high school students find this practice in their weekly homework. I also include conversions from fractions to decimals and percentages.
In addition, this practice prepares students to solve equations with fractions. It also increases student confidence and success in other math content such as life skills, probability, geometry, state testing, college entrance exams, and more.
B. Strategies for Equations with Fractions
Likewise, what are time-saving strategies that help students jump the hurdles in equations that include fractions? Let’s consider the following.
- 1. Include student review and practice that emphasizes fraction operations.
This could be in the form of bell work, homework, quizzes, and tests. An easy method: print off a fraction practice page that includes 20 problems. On each day, students complete one problem from that sheet.
2. Provide easy-access posters that illustrate steps for completing fraction operations.
3. Provide opportunities for students to teach each other, using illustrative posters.
Are you looking for more strategies for multi-step equations with fractions? Click on the following title link below.
Equations with Fractions: How to Successfully Solve
C. Resources to Prepare for Equations, Fractions, and Parentheses
Are you looking for time-saving resources to re-teach fraction operations to high school students? No problem, I’ve got you covered. Below are two resources that will provide both detailed poster examples and practice. Just print-and-go!
Fractions, Decimals, and Percents Practice for High School Review

Fraction Operation Puzzles and Posters: Steps for Solving

#2 – A Fraction Beside a Parenthesis
Now, let’s look at an example that includes an equation with a fraction, and parenthesis. Such a problem can evoke significant anxiety in the average math student. On the other hand, if a student is aware that the denominator may be “removed,” the student will demonstrate less anxiety with a problem similar to this example.
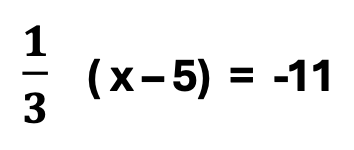
How does one solve the problem? There are two basic steps. Sounds easy, right?

Before solving for x, consider the significant features illustrated above in the first step.
- 1. Color coding helps students recognize the L.C.M. from the original fraction.
2. The purple L.C.M. inside the green box illustrates the L.C.M. in fraction form. Though examples elsewhere may illustrate whole numbers as the L.C.M., students can become confused. Let’s look an example below.
The Original Problem
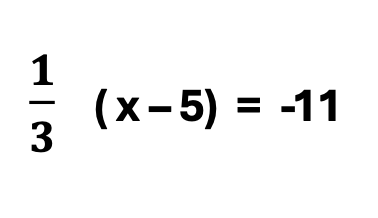
Multiplying the L.C.M. as a Whole Number Times a Fraction
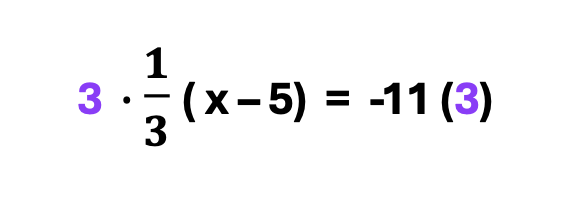
Do you see how some students may wonder whether to multiply the L.C.M. of 3 times the 1 in the numerator, or the 3 in the denominator?
Multiplying the L.C.M. as a Fraction Times a Fraction
Furthermore, notice how the purple fraction form of the L.C.M. in the green box below, clearly represents what part of it aligns with 1/3.


#3 – An Equation with More than One Term in the Numerator
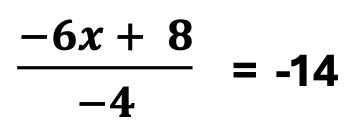
Furthermore, let’s consider an equation with more than one term in the numerator. In this step, the number in the denominator is -4. Occasionally students will question the L.C.M. value asking whether the L.C.M. should be negative or positive. The answer: If the number in the denominator is negative, the L.C.M. will also be negative. Also, add that the L.C.M. on the other side of the equation will also remain negative. See the example below.
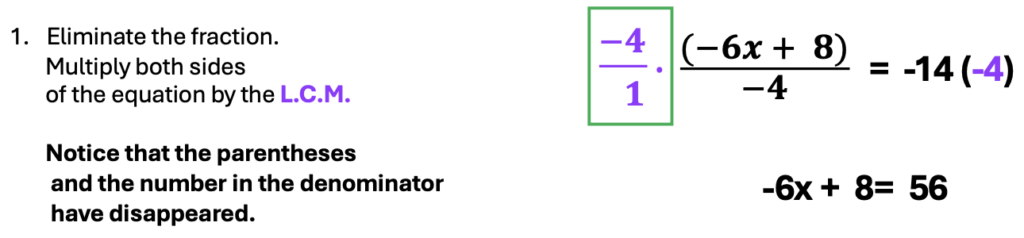

#4 – Two Fractions on the Same Side of the Equation
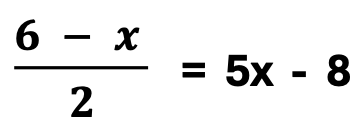
In addition, this example illustrates another common misunderstanding. Though students understand that what happens on one side of the equation must happen on the other, they are known to wonder what to do with more than one term, such as 5x – 8. It is important to emphasize the placement of parentheses around the remaining terms with the L.C.M. on the outside of the parenthesis, followed by distributive property into EVERY TERM INSIDE THE PARENTHESIS! I capitalize the prior statement, as I observe students who may distribute into the first term, though they forget the remaining terms.


Looking for a way to simplify your instructional time on this topic?
Furthermore, equations that include fractions and parentheses take a lot of instructional time.
Time-Saving Tips
- 1. Before covering equations with fractions, provide fraction operation review and practice before teaching this topic.
2. Provide three to five short, easy-to-understand, equations that include fractions.
3. After students understand the easy problems and discover that these steps result in a simple equation, move on to more challenging problems.
4. When illustrating the more complex problems, end the illustration after the fractions have “disappeared,” and move on to others. Inform students to leave spaces between each problem to return and finish the equation. This will provide more time to include more illustrations that include equations with fractions.
Conclusion
In conclusion, an awareness of student readiness, common misperceptions, and strategies to address these misconceptions are meaningful when teaching students how to solve problems with equations, fractions, and parentheses.
Looking for More Materials?
Click the button below to view more of my educational resources!
