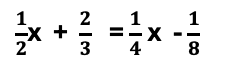Fractions! Worse yet, equations with fractions! Where to begin? No worries. In this post, you will discover strategies that will allow you to solve equations with fractions, successfully.
#1 – How to Prepare
Are you ready to solve equations with fractions? Let’s make sure.
A review of the following concepts will prepare you to make sense of the steps for solving equations with fractions. Many of these concepts you are familiar with will be applied when solving equations with fractions.
First: Follow all the detailed steps you used in the previous equations.
Skip a space between each step.
Second: Review the following fraction concepts.
1. Any real number over 1 represents the real number. For example, 32/1 = 32
2. Steps for solving fraction operations
3. How to find the least common multiple
4. How to reduce fractions to the lowest terms.
Furthermore, if you are looking for an overview of fraction operations, click on the title below:
#2 – Equations with Two Terms
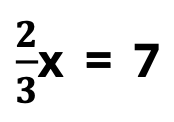
To begin, the most common question you will likely ask is,
“Where do I begin?”
If you are looking for the answer online, you might find a response such as,
“Clear the denominator by multiplying the least common multiple”
Then again, you may wonder,
“What does it mean to clear the denominator?
A. Equations with Fractions: Two Terms
First, take a look at an equation with only two terms.

Next, complete the following steps:
1. Skip a space and re-write the problem.
2. Write 7 as a fraction, 7 / 1 as done in the example below.
This helps the problem look more uniform and provides a visual reminder that the seven is in the
numerator and the one is in the denominator.
3. Determine the least common multiple, which is 3.
4. Now, multiply the least common multiple with all terms on the right and left sides of the equation.
5. Simplify each new fraction.
6. Bravo! Next, solve for “x”.
Now you have learned what clearing the denominator means. Better yet, you have observed what a wonderful strategy this is as this process gives you back the type of equation you know and love … without the fraction!
In addition, it is important to recognize the importance of writing the whole number in fraction form.
Multiply the least common multiple by writing the whole number in fraction form.
This method helps you keep top and bottom numbers lined up.
B. Equations with Fractions: Fraction Equals Fraction
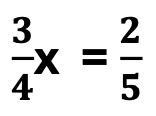
Next, in the following equation, both terms are fractions on both sides of the denominator. We will follow very similar steps with this problem as well.
Likewise, you will notice that the steps below are the same as the previous problem
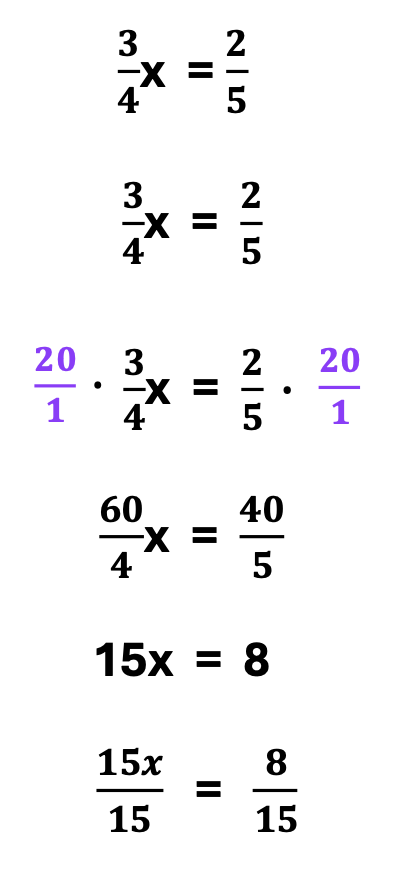
1. Determine the least common multiple, which is 20.
2. Now, multiply the least common multiple with all terms on the right and left sides of the equation.
3. Simplify each new fraction.
4. Bravo! Next, solve for “x”.
#3 – Equation with Three Terms
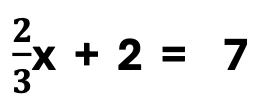
Furthermore, you may consider multiplying each term by 3 in the equation above. However, I recommend isolating 2/3x, first. See the illustration below.
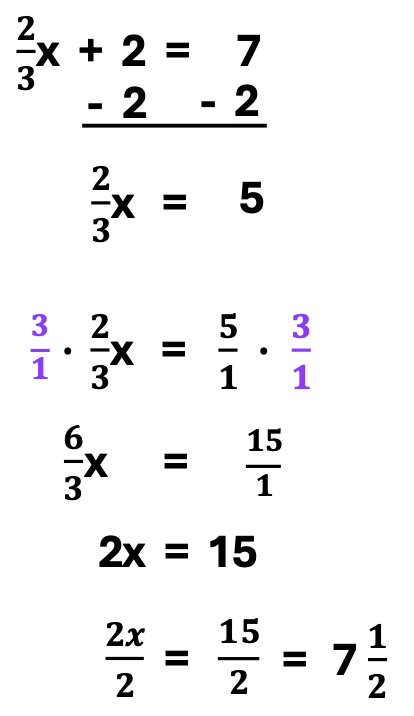
Likewise, notice the repeating steps:
1. Determine the least common multiple, which is 3.
2. Now, multiply the least common multiple with all terms on the right and left sides of the equation.
3. Simplify each new fraction.
4. Next, solve for “x”.
You are becoming an expert, already!
#4 – Equation with Four or More Terms
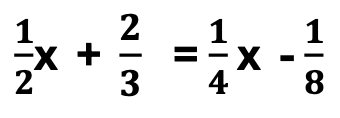
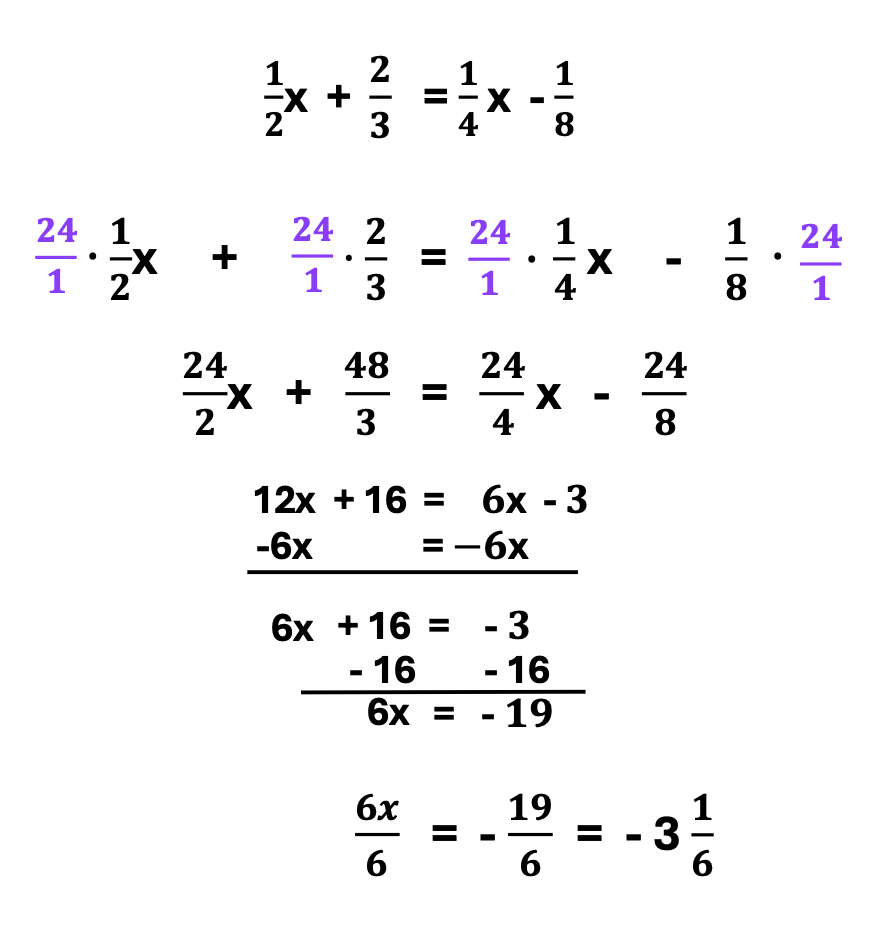
You’ve got this! Just repeat the steps.
1. Determine the least common multiple, which is 24.
2. Now, multiply the least common multiple with all terms on the right and left sides of the equation.
3. Simplify each new fraction.
4. Next, solve for “x”.
Conclusion
By following four basic steps, you can easily solve equations with fractions.
1. Determine the least common multiple.
2. Multiply the least common multiple with all terms on the right and left sides of the equation.
3. Simplify each new fraction.
4. Next, solve for “x”.

Squirrel image created by: PrintsnPencils
Looking for More Materials?
Click the button below to view more of my educational resources!