What are domain and rational expressions? Find the domain? Good news! Though the words may be unfamiliar, the big idea is not new. You’ve got this! Keep reading and discover how to successfully find the domain of rational expressions.
Contents
- 1. What is a Rational Expression?
2. Similarities Between Rational Expressions and Fractions of Our Past
3. Descriptions of the Domain
4. Finding the Domain
5. Examples
Conclusion
1. What is a Rational Expression?
In simple terms, a rational expression is a fraction with algebra terms which may be found in both the numerator and denominator. Terms in the rational expression may include numbers, variables and exponents.
Yes. Rational expressions are like fractions dressed up with ties, and bows sprinkled with glitter. Below are examples.
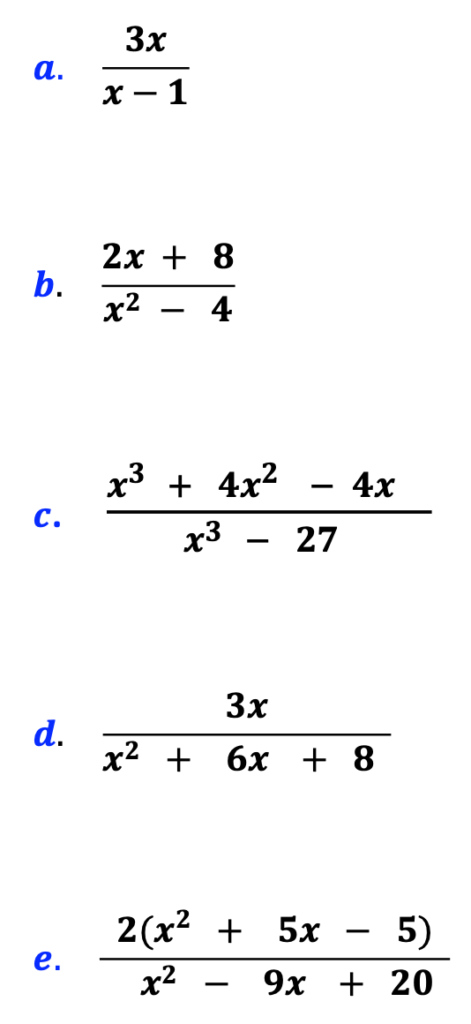
2. Similarities Between Rational Expressions and Fractions of Our Past
First, both types of fractions can be reduced to the lowest terms. In Algebra, we may substitute the words, “Simplify the expression,” to mean the same thing. We are simply breaking the expression into its smallest terms.
Second, rational expressions can be added, subtracted, multiplied, and divided just like fractions from our past.
Third, rational expressions and previous fractions cannot contain a zero in the denominator. Observe the details below.





3. Descriptions of the Domain
When you are introduced to rational expressions, the term, “domain,” will be referred to. The domain may be described as:
All real numbers that when used in the denominator will NOT result in zero. This is a key concept to remember for this topic and other topics that follow in regards to rational expressions.
When graphing a linear equation, the domain represents all the possible x-values of that function.
For example, you may remember plotting points on the Cartesian Plane. You may have used ordered pairs or a t-chart which provided x and y values for placing points on a graph. The x-values represent the domain.
Oh, by the way, the y-values represent the range.
4. Finding the Domain
Now that we know what a rational expression and domain is, we are ready to find the domain.
This is accomplished by finding out what the domain cannot be. This means determining what numbers will cause a zero to occur in the denominator. After finding the number or numbers that will cause zero to result in the denominator, the remaining numbers are those that will not cause the denominator to go to zero. These numbers are referred to as, “All Real Numbers,” the numbers that represent the domain.
5. Examples
The following are detailed examples.
Example # 1


Example # 2
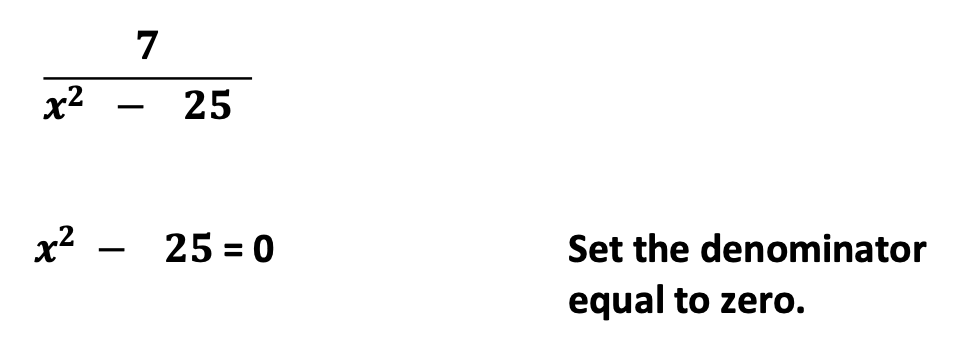
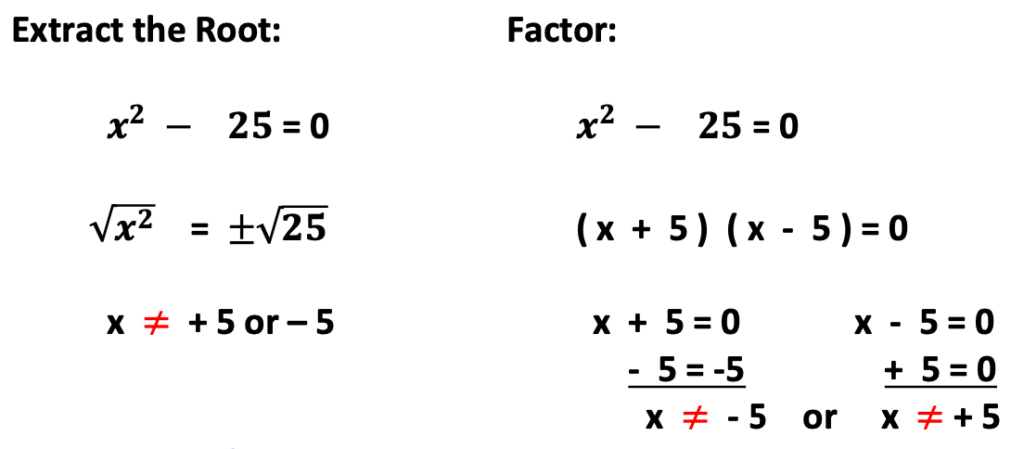
Once again, you will observe that all numbers could be used for “x” except 5 and -5. Such numbers would cause the denominator to become zero.
Example # 3
Viewing this and the following example, you will notice two ways to find the domain. One way is to use the method for extracting the root. Factoring is another method that may be used. Either method will result in the same answer.


Example # 4
Furthermore, the method of extracting the root may also be used with rational expressions which include a rational expression with two terms in which one is a cube. Observe the method used in the next two examples.


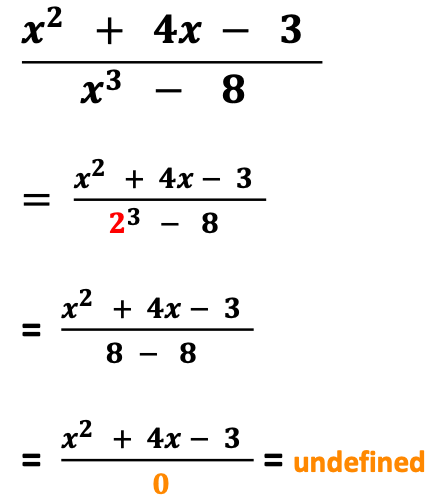
Example # 5

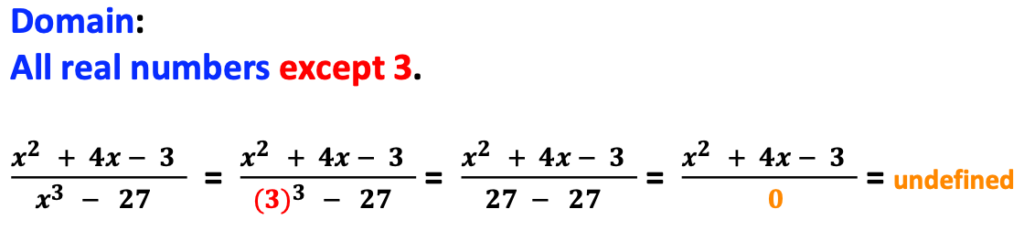
Example # 6
In this example, you would simply factor the trinomial. Though the factor pairs are both (x + 1), there is only one domain of -1.

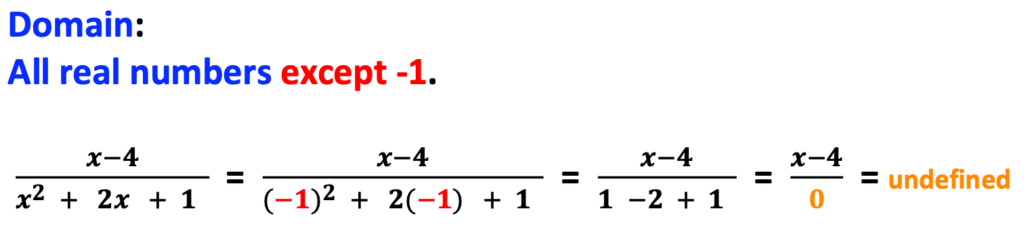
Example # 7
In this example, notice the detail involved in proving 4 and 8 are not part of the domain. Careful detail is everything!


Conclusion
Though finding the domain is not difficult, it is a very important skill to understand before simplifying rational expressions.
You may also be interested in the following product located at my Teacher’s Pay Teachers Store,
“How to Find the Domain of Rational Expressions.”
See the link below.
https://www.teacherspayteachers.com/Store/Bonnie-Stephan


Looking for More Materials?
Click the button below to view more of my educational resources!
