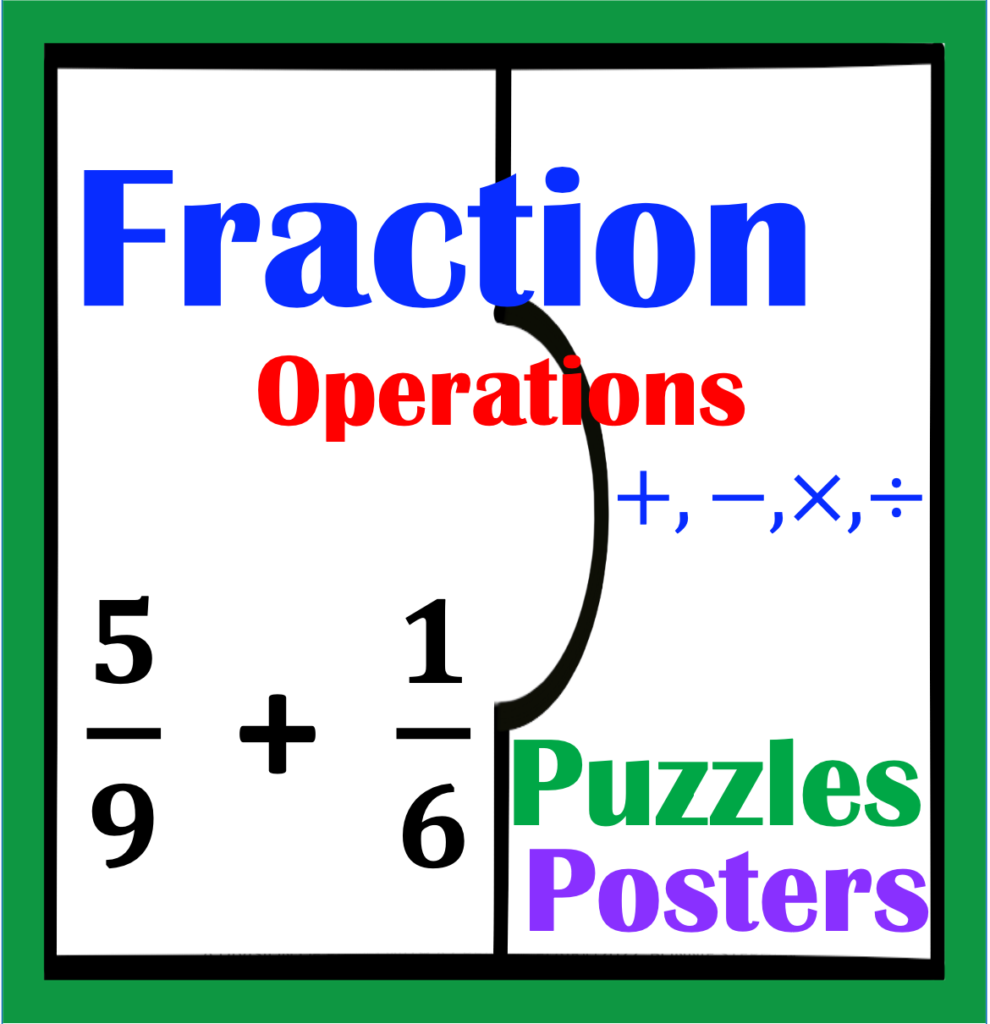
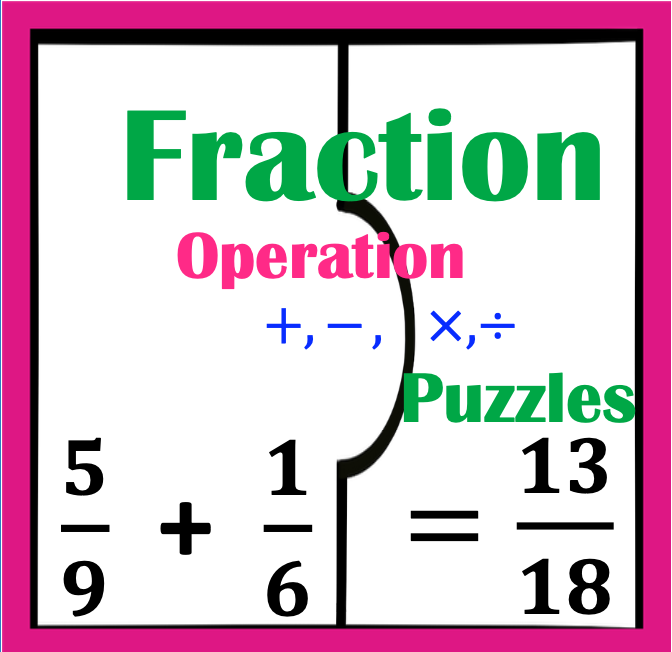
Are students becoming confused with methods used for solving integer operations? Have you moved on to order of operations and noted that student frustration only becomes worse? I’ve been there. However, my experience only led me to great observations and discoveries which I will share in this and future posts. This short post is provided as an introduction explaining how to teach integers for success for order of operations, part 1.
- 1. My Favorite Introductions for Student Success with Integers
2. Student Challenges With Integers and Order of Operations
3. A Proven Method to Overcome Those Challenges
1. 1. My Favorite Introductions for Student Success with Integers
Thanks to the internet, finding ways to introduce integers is quite plentiful. Some of my favorites include an introduction to absolute value, real-life examples, use of counters with positive and negative signs, and practice with numbers on both horizontal and vertical lines. The more my students can relate to these numbers, the easier it is to experience success with integers.
For more details regarding strategies for introducing integers, click on the link below: Introducing Integers: Best Methods with Negative and Positive Numbers.
: How to Teach Integers for Success for Order of Operations, Part 1
These methods appear to work great with problems such as -6 + 2 or -4 – 1.

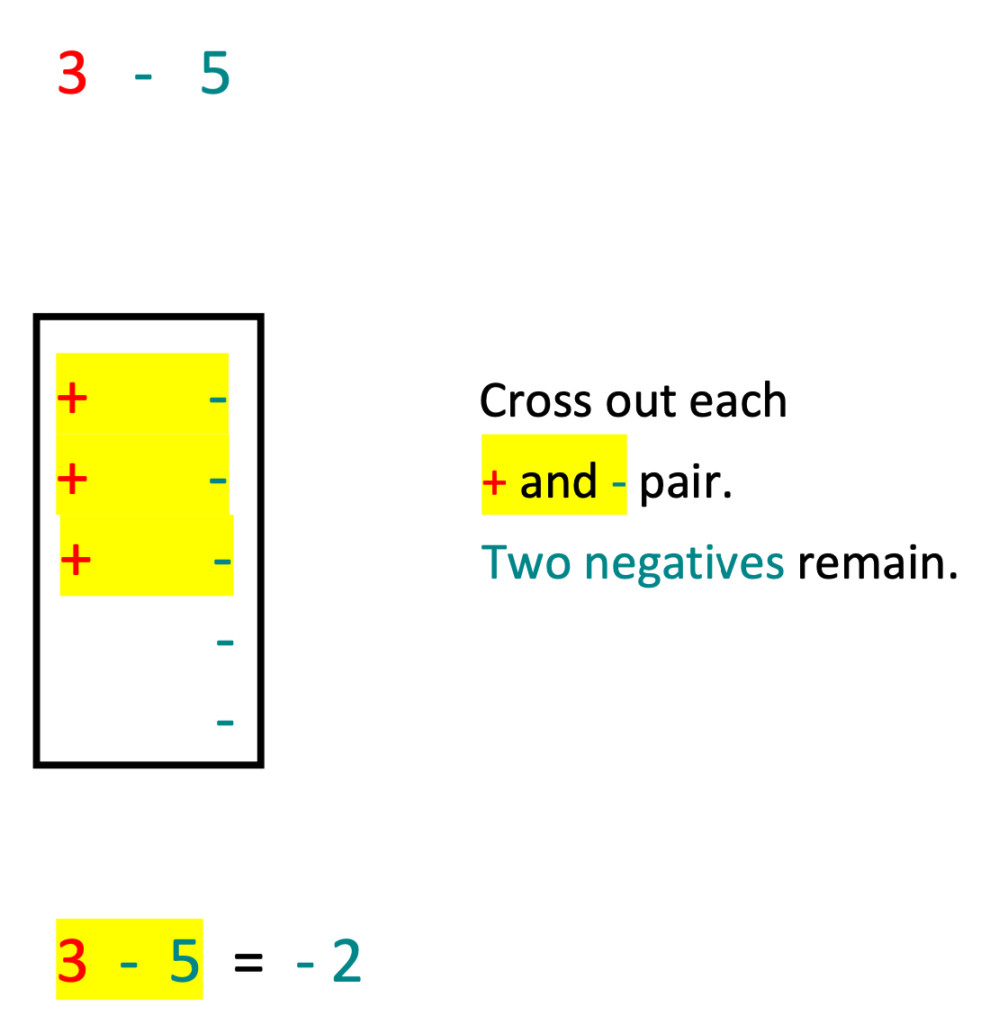

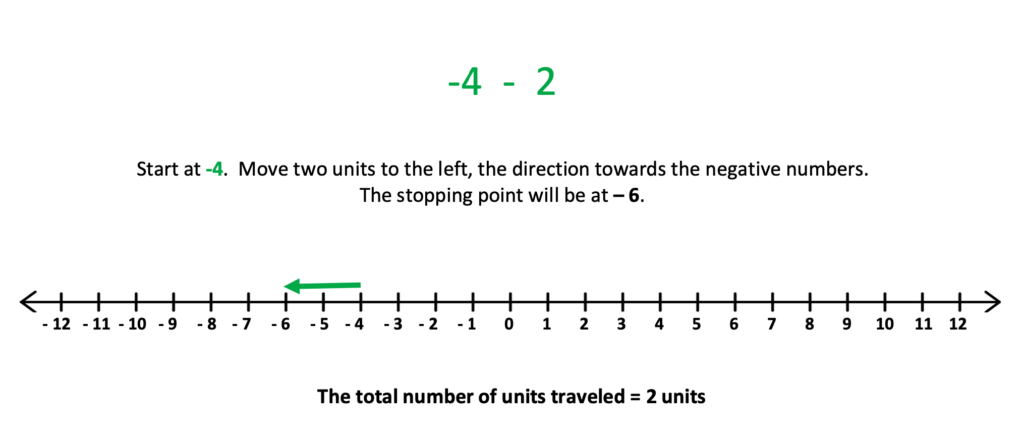
2. Student Challenges With Integers and Order of Operations
Though the methods for introducing integers went well, I did discover students experiencing difficulties with double signs in between numbers such as 7 – – 3. Parentheses within the expression also appeared to cause confusion, such as 8 – ( – 3). Though I utilized the rule method, I found that many of my students became overwhelmed with the words.
When moving on to problems related to order of operations it was plain to see that students became even more confused with such problems as -7 + (-3)4 – 3.
“Multiply? Subtract? Then, add? Where do I start?”
Maybe you have been there or you are there right now. If you teach students with learning disabilities, language processing issues, or students who are significantly visual learners, you know what I am talking about.
You can only verbalize the rules and phrases so long until at your feet is a puddle of tears as you believe in your heart of hearts that there has to be a better way. This experience only seemed to dampen student success with integers.
3. A Proven Method to Overcome Those Challenges
Teach Integer Operations for Multiplication and Division
I knew that I needed to address the strategy for multiplication, and division before explaining a strategy that has proved most effective for integer operations and more challenging order of operation problems.
So what is the most effective and the least confusing strategy to use with integers for multiplication, division, and order of operations? How can students experience success with integers and order of operations?
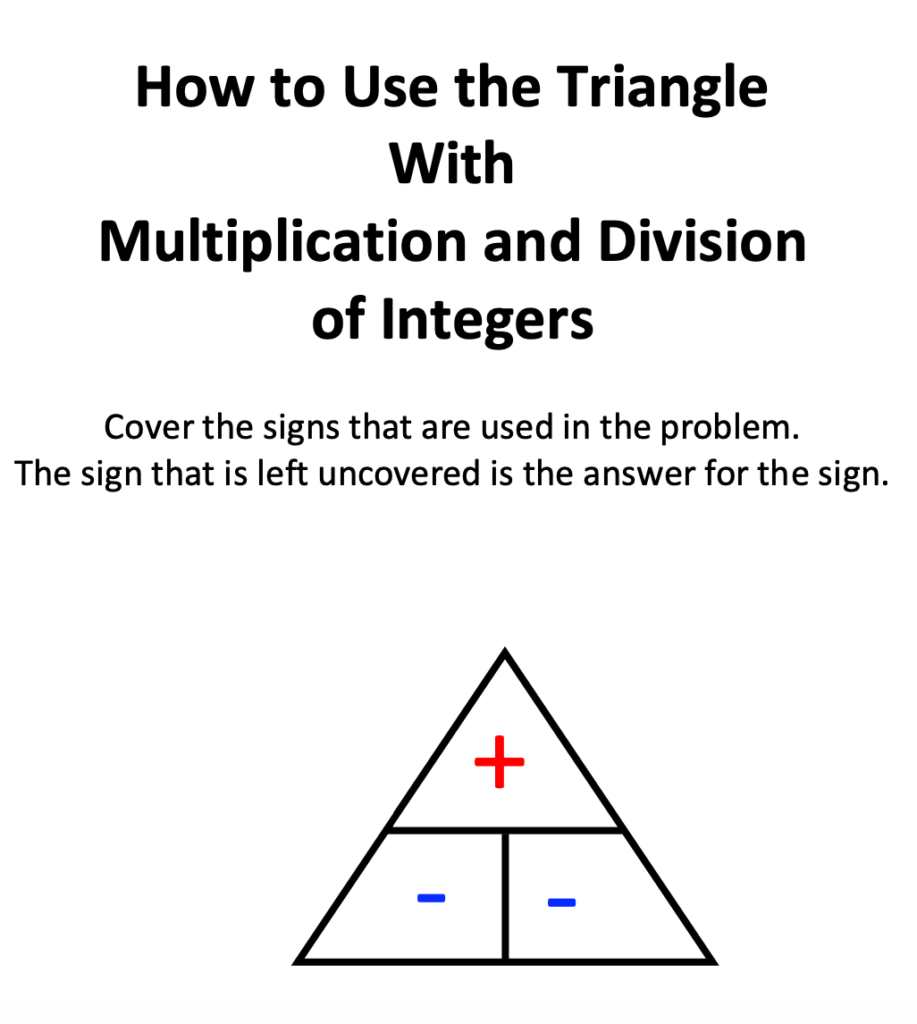
You may have guessed it and may have even used it. Yes. It is the triangle method. My students absolutely love this!
Why do I use the triangle? For my students with learning disabilities, language processing challenges, or students who are significantly visual learners, this is a total game changer. If you are not familiar, see the examples below:
Another benefit of introducing the triangle method is that they do not have to learn “rules” for multiplying, dividing and distributive property, though intuitively learn the rules by using the triangle.
For example, how many times have students become confused between the rules for adding and subtracting with the rules for multiplying and dividing?
Might I add, while introducing multiplying and dividing, continue to review adding and subtracting integers such as -5 + 3. Once again, If students use the triangle method and continue to review adding and subtracting, there will be greater success with integer operations and solving future order of operation problems.

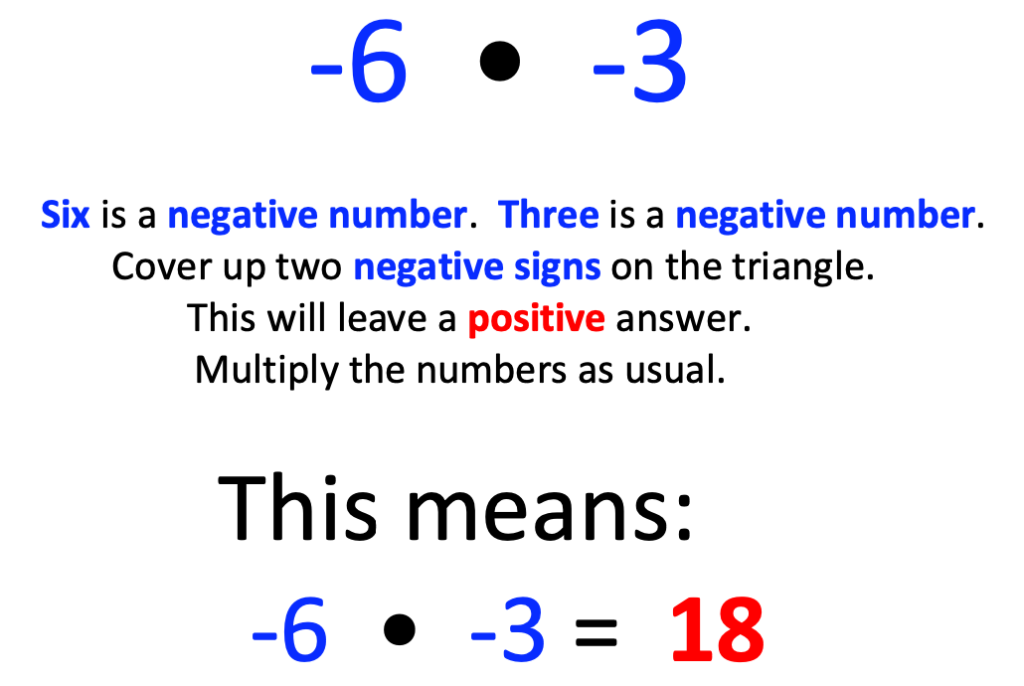


In the following posts, you will find specific, step-by-step instructions for success with integers which will also provide student confidence when working order of operation problems.
Types of problems presented in the next post: 7 + (-3) and 4 – – 8.
Conclusion
Helping students develop an understanding with simple adding and subtracting of integers with the introduction of absolute value, real-life examples, use of counters with positive and negative signs, and practice of both horizontal and vertical lines creates a conceptual understanding of integers. Next, instruction with multiplying and dividing integers lays a great foundation upon which to learn other strategies which pave the way for success with order of operation problems.