Are students becoming confused with methods used for solving integer operations? Have you moved on to order of operations and noted that student frustration only becomes worse? I’ve been there. However, my experience only led me to great observations and discoveries which I will share in this and future posts. This short post continues to explain and illustrate how to teach integers for success for order of operations, part 2.
- 1. Why Use this Method for Teaching Integers?
2. Before 7 + (-3) and 4 – – 8
3. Sign, Sign, and a Triangle
4. Sign, Parenthesis, and a Sign
5. A Problem with a Common Question
1. Why Use this Method for Teaching Integers?
Though the methods for introducing integers went well, I did discover students experiencing difficulties with double signs in between numbers such as 7 – – 3. Parentheses within the expression also appeared to cause confusion, such as 8 – ( – 3). Though I utilized the rule method, I found that many of my students became overwhelmed with the words.
When moving on to problems related to order of operations it was plain to see that students became even more confused with such problems as -7 + (-3)4 – 3.
“Multiply? Subtract? Then, add? Where do I start?”
Maybe you have been there or you are there right now. If you teach students with learning disabilities, language processing issues, or students who are significantly visual learners, you know what I am talking about.
You can only verbalize the rules and phrases so long until at your feet is a puddle of tears as you believe in your heart of hearts that there has to be a better way!
2. Before 7 + (-3) and 4 – – 8
1st: Begin with an introduction to absolute value, real-life examples, use of counters with positive and negative signs. Include the use of both horizontal and vertical lines.
For more details on these methods, refer to a prior post, Introducing Integers: Best Methods with Negative and Positive Numbers which may be found by clicking the link below:
https://ledtodiscover.com/algebra/introducing-integers-best-methods-with-negative-and-positive-numbers/
2nd: After students are able to conceptualize the meaning of integers using the above described methods, begin teaching multiplication, division with the triangle. This is been quite the game changer for my students. It is also particularly useful for students with language processing challenges and learning disabilities in math.
To learn about this very important component, I refer you to, “How to Teach Integers for Success for Order of operations, Part 1 which can be found by clicking the link below:
3rd: When students can conceptualize, multiply, and divide integers, they are ready to leap into the great adventure of double integers, such as 7 + (-3) and 4 – – 8.
Furthermore, the examples you will observe in this post will be related to a specific type of integer problem.
Double signs will only occur between two numbers.
No negative signs will be in front of the first number. These are problems that will be illustrated in the next post.
All examples will result in positive answers.
The method I am about to share has significantly made a huge difference in student confidence working order of operation problems with double signs, parentheses and distributive property.
Most students would at this point look at the problem below and feel overwhelmed with different signs, parentheses and numbers. However, at the end of this post you will discover how the strategies that follow, literally shrinks this problem down in size.
Ready or not, let’s begin!

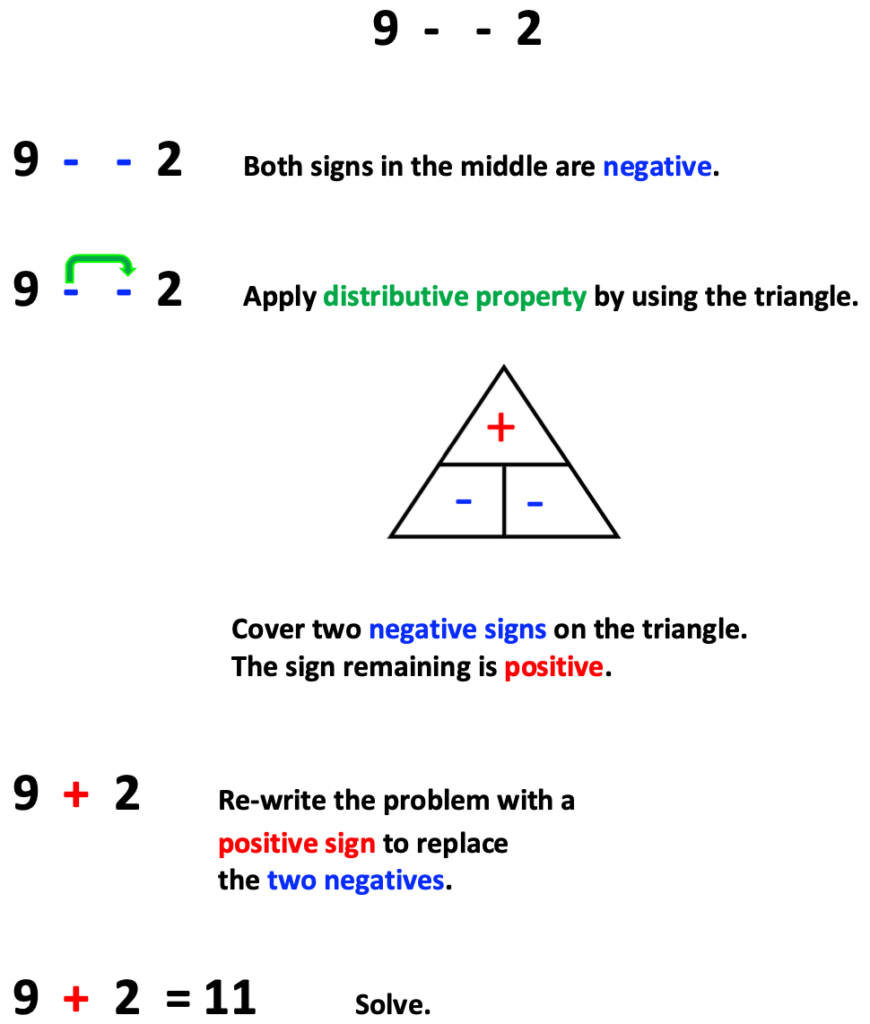
3. Sign, Sign and a Triangle
You will notice that the problem below includes two negative numbers in the middle. When this occurs, the problem may be simplified by using distributive property as illustrated below. The triangle is used as a tool to help students determine the sign that will be used in the simplified expression.
You will notice that the problem below has a negative and positive sign between two numbers. This problem is simplified using distributive property as well.
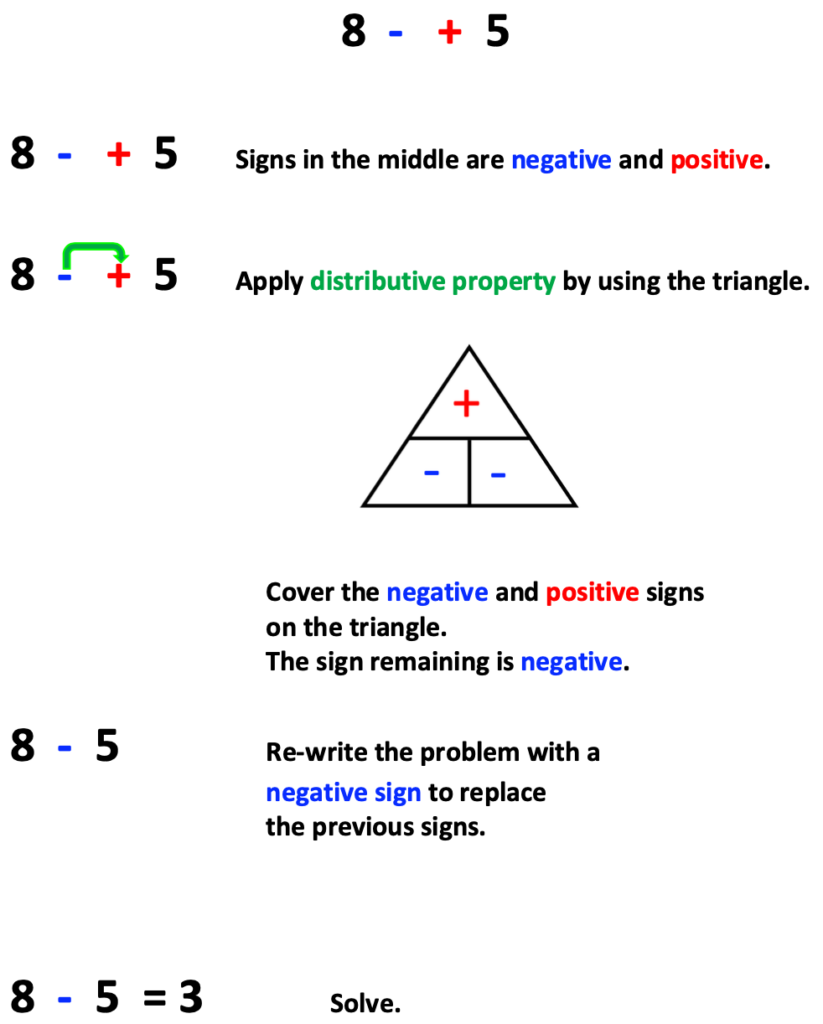
Note that the problem directly above and the one below contain the same signs though in reverse order.
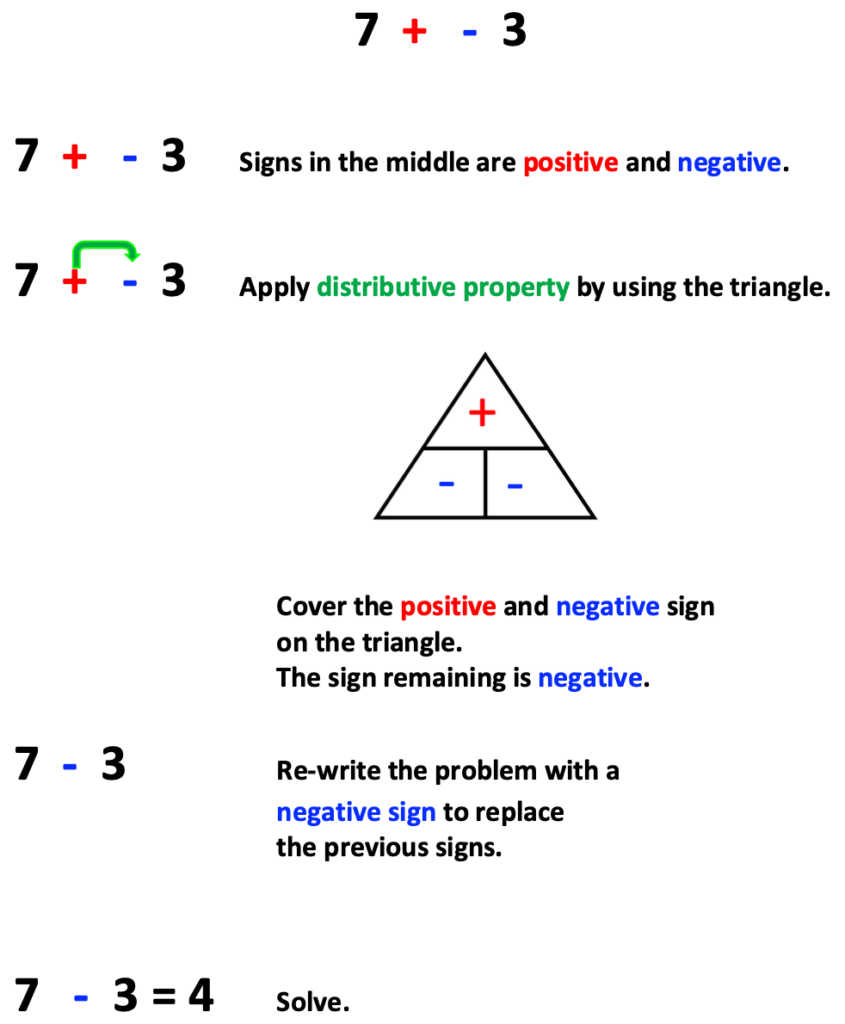
As students practice this method using distributive property, what once looked mind-boggling, now looks easy. After completing distributive property, they discover the next step is simple addition or subtraction.
3. Sign, Parenthesis and a Sign
Oh, the ever-important parenthesis between signs and numbers! This is order of operations in its infancy!
The good news: the method for simplifying the expression is the same! Observe the steps for solving the problem below.

The next two problems are solved using the same methods, though the signs are different.

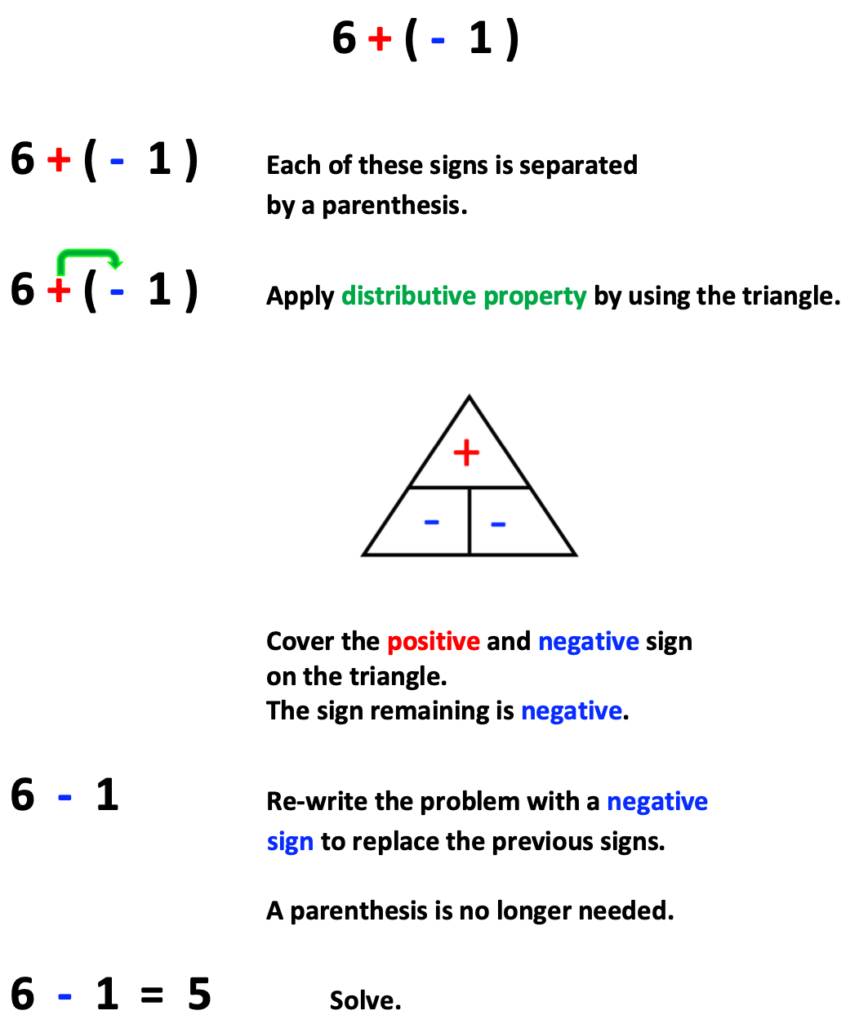
5. A Problem with a Common Question
Students, once comfortable with distributive property, will usually zip through problems like the ones in this post. Distribute, use the triangle and do some first grade math! Yippee!
Hurrah! Students are moving towards success with integers!!!
And then it happens. They arrive at a problem in which there is no sign directly in front of the number and that number is in parenthesis. Panic sets in and they freeze, hand barely raised.
This is a great time to take a restroom break, stop by the drinking fountain, and review deep breathing technics. Yes, empty, refill, and oxygenate.
Upon returning to the room, I recommend reminding students that a number inside a parenthesis is positive unless a negative number is inside the same parenthesis as the number.
For example, in 8 – ( -1 ), the negative and the number one are both inside the parenthesis, meaning the number inside the parenthesis is negative one.
On the other hand, in 8 – ( 1), there is no sign in front of one. This means that the one is positive. I will also explain this as one having an “invisible” positive sign in front of it.
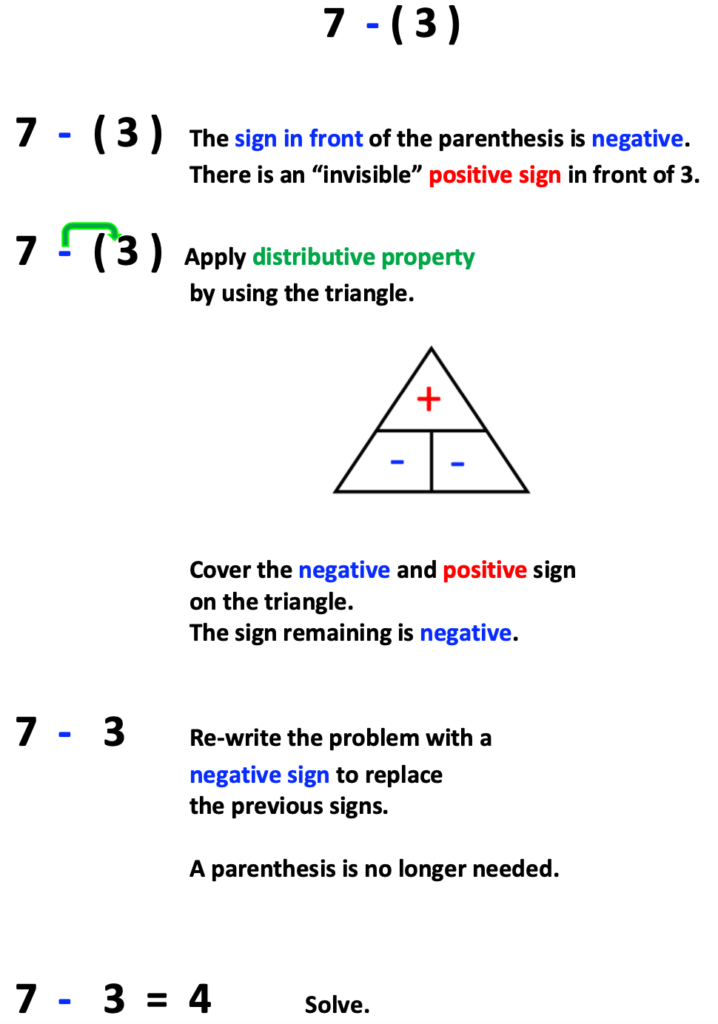
I almost forgot! At the beginning of this post, I shared a multi-step expression with many signs and parentheses. Below are the steps for solving it. Pay close attention to the use of distributive property and how it is used as a strategy for solving integers within itself! Quite beautiful!

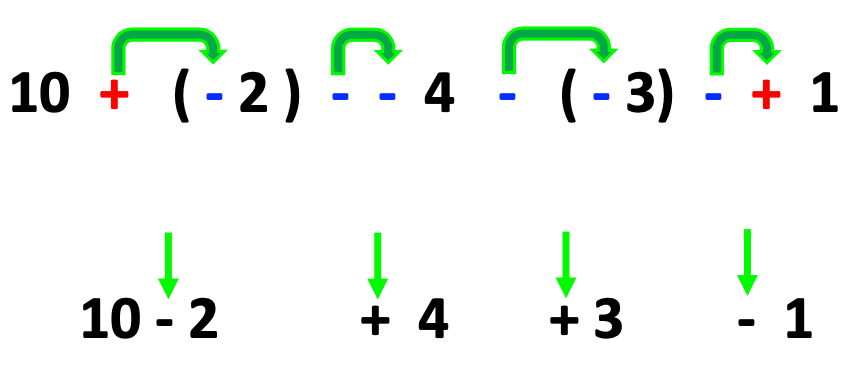
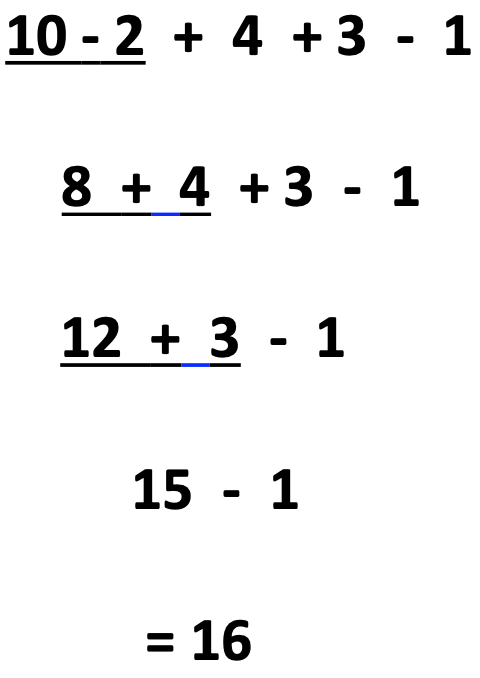
Conclusion
Students need to understand how to use distributive property with use of the triangle with integer problems. These strategies will also be applied in the next post. Next, instruction with multiplying and dividing integers lays a great foundation upon which to learn other strategies which pave the way for success with order of operation problems as discovered in the example above.
Types of problems presented in the next post: -7 + (-3) and -4 – – 8. These are problems that include signs in the middle of two numbers though also include a negative sign in front of the first number.
Prior to moving students to these types of problems, be sure they completely understand how to solve problems addressed in this post and prior integer concepts practiced with number lines and other visual strategies. Introducing new concepts too quickly may cause some students to get confused and then frustrated. Always remember it is better to review or provide review practice than to move forward too quickly to experience success with integers.
A flower must bud before it blossoms.