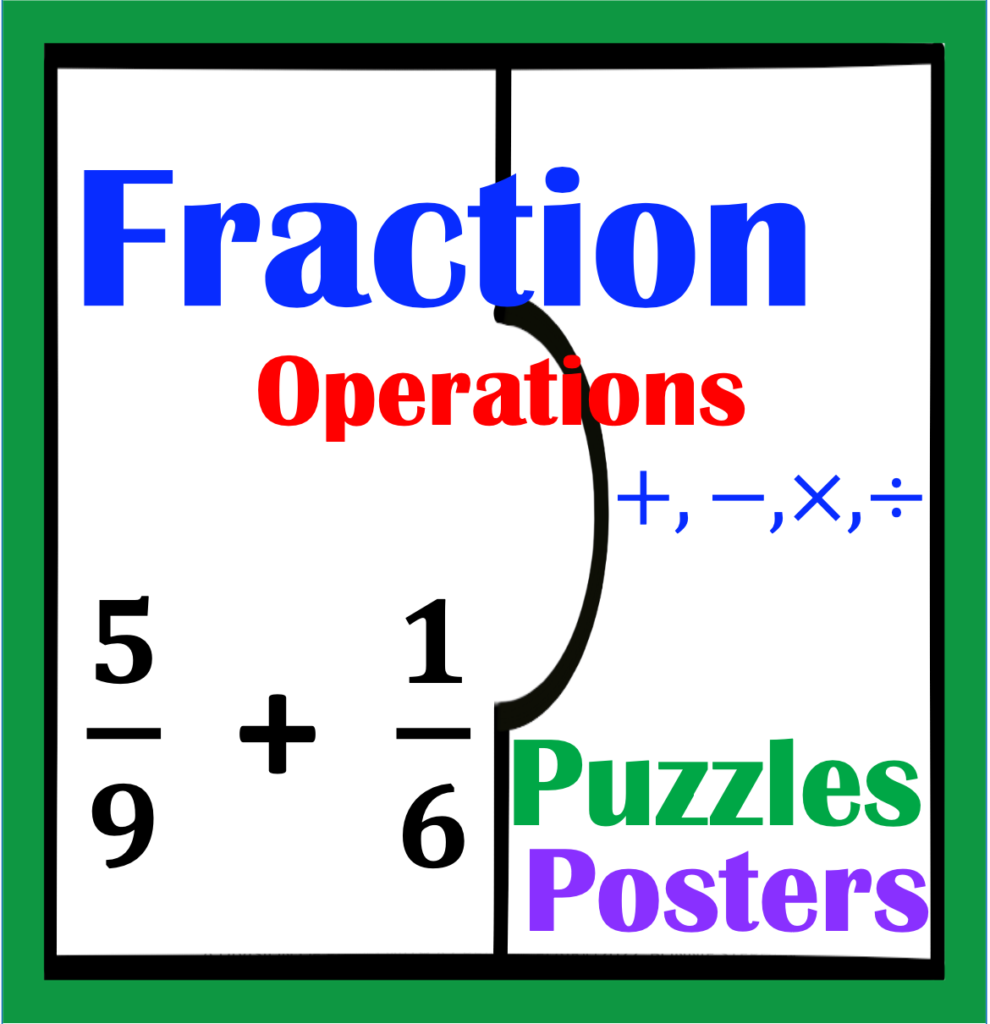
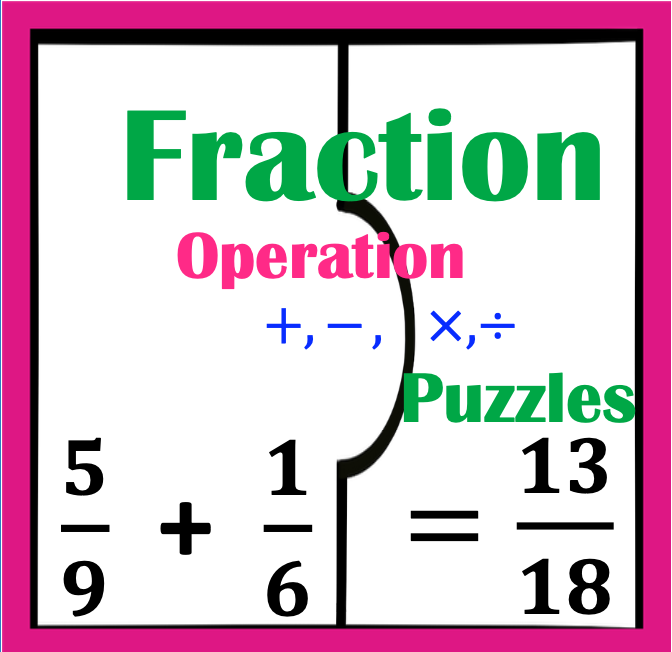
Are you looking for integer strategies that are not only effective but also anchor student success with order of operations? If this describes you, keep reading to discover how to teach integers for success for order of Operations, Part 3.
In addition to reading this post, you may also want to read the following prior posts on this subject:
1. Introducing Integers: Best Methods with Negative and Positive Numbers
2. How to Teach Integer Operations for Success for Order of Operations, Part 1
3. How to Teach Integer Operations for Success for Order of Operations, Part 2
Contents:
- 1. Why Use This Strategy?
2. When the First Number is Negative
Conclusion
Why Use This Strategy?
First: By using distributive property when teaching integers, students quickly grasp integer operations with double signs and parenthesis. This provides a very effective method that promotes carry over for success for order of operations.
Second: This has been a major game changer particularly for my students with learning disabilities, language processing disorders, and highly visual learners. Once my students have learned integer operations, they are ready to complete problems such as the one below.
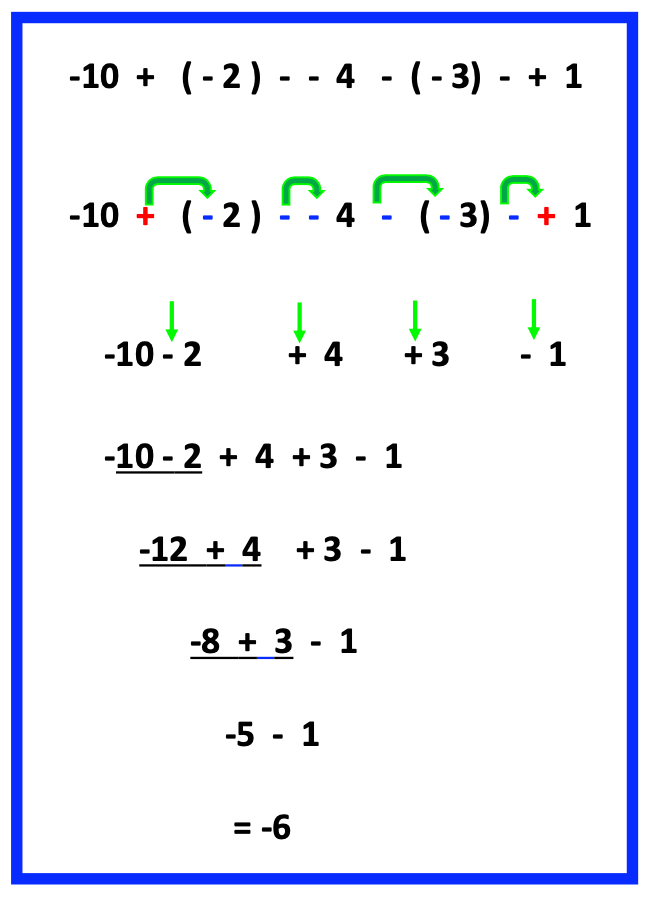
When the First Number is Negative
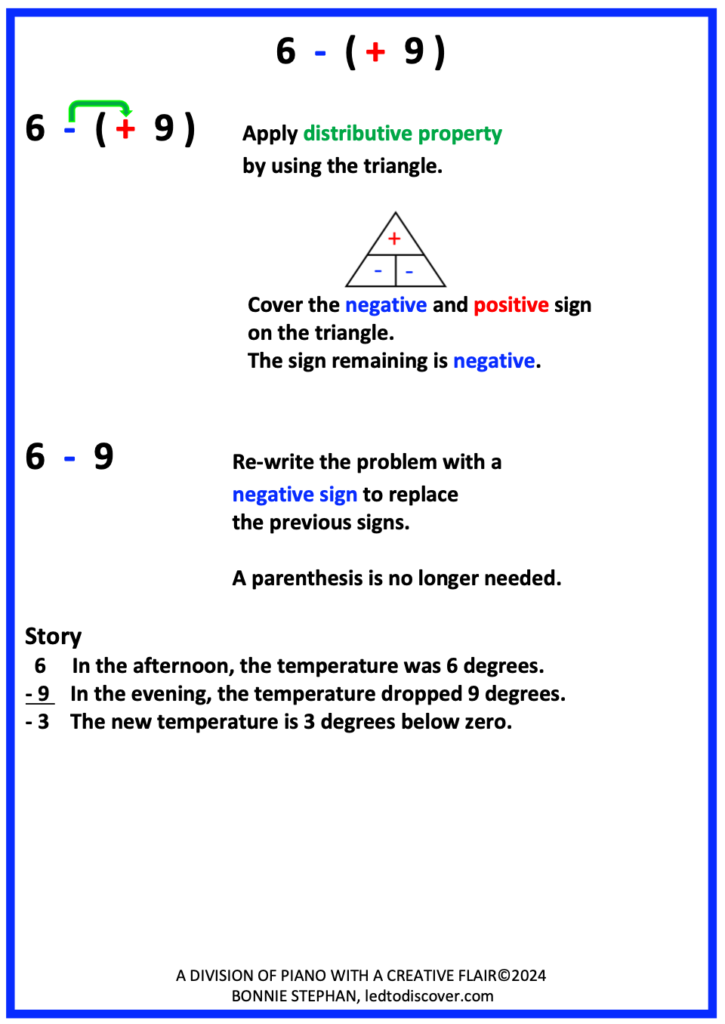
In the example below, notice that there are two signs in between the -9 and 3. When students have been practicing distributive property, they will most likely perform distributive property before being concerned with the negative in front of the first number.
After using distributive property for the signs in the middle, they will recognize that the problem turns into a problem they have already practiced with number lines or other strategies: -9 -3.
How awesome! By first applying distributive property, the result is a problem they recognize, and solve with ease.

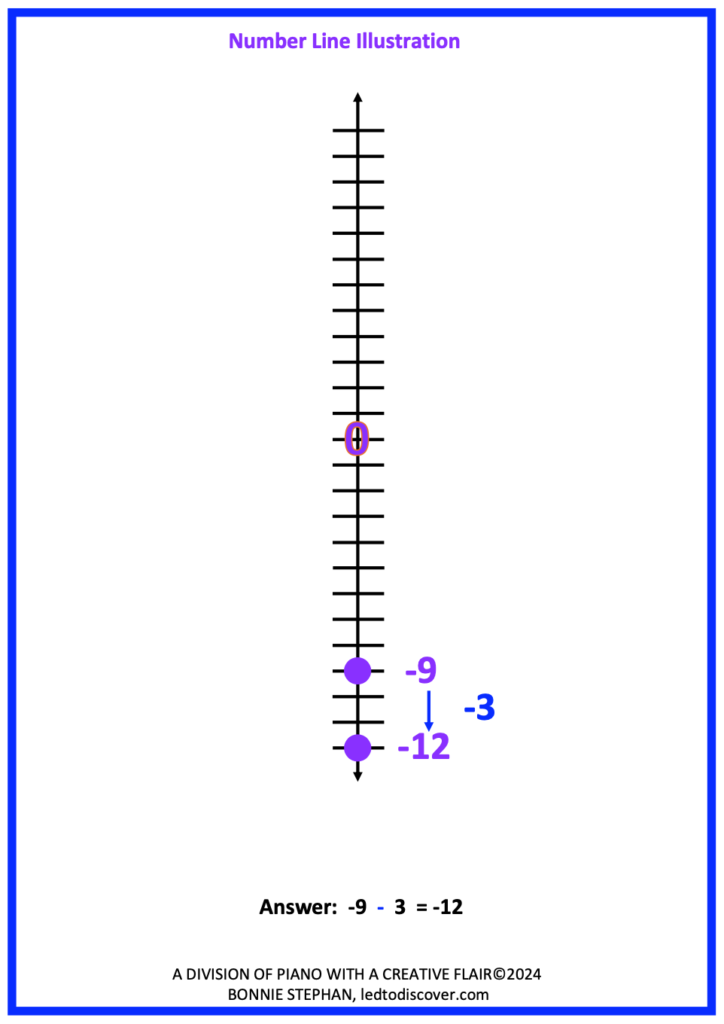
Furthermore, continue to apply real events to integer problems. As students calculate and process problems such as-9 – 3, it is important for students to include the following:
1. Write the problem vertically. This is incredibly helpful, as it prepares students to solve equations when different signed numbers appear when solving equation. See the illustration below.
2. Write three to four sentences expressing the meaning of the integers.
3. Demonstrate the expression on a number-line. Depending on the theme of the sentences written, a vertical or horizontal number line may be more meaningful. For example, the sentences related to the expression above is related to movement that may best be visualized on a vertical number line vs. a horizontal one.

The next two examples illustrate the process of solving problems when an expression contains a sign, a parenthesis, and a sign. Notice that both of these examples contain short sentences related to temperature change. As students are likely to visualize a thermometer in vertical form, the number-line used is also vertical.

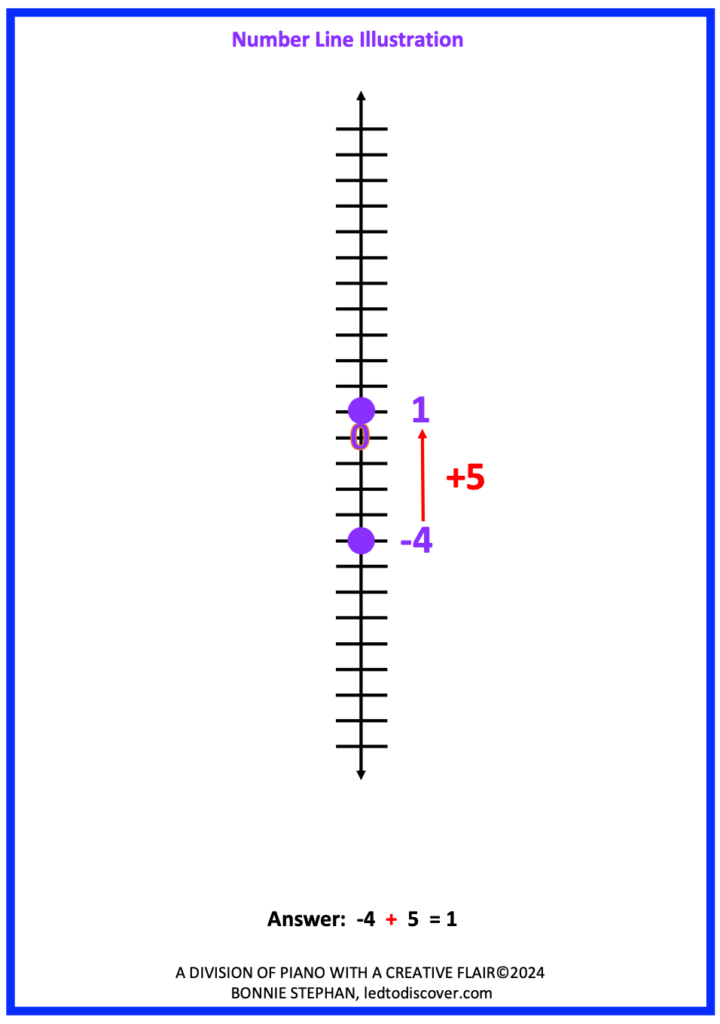
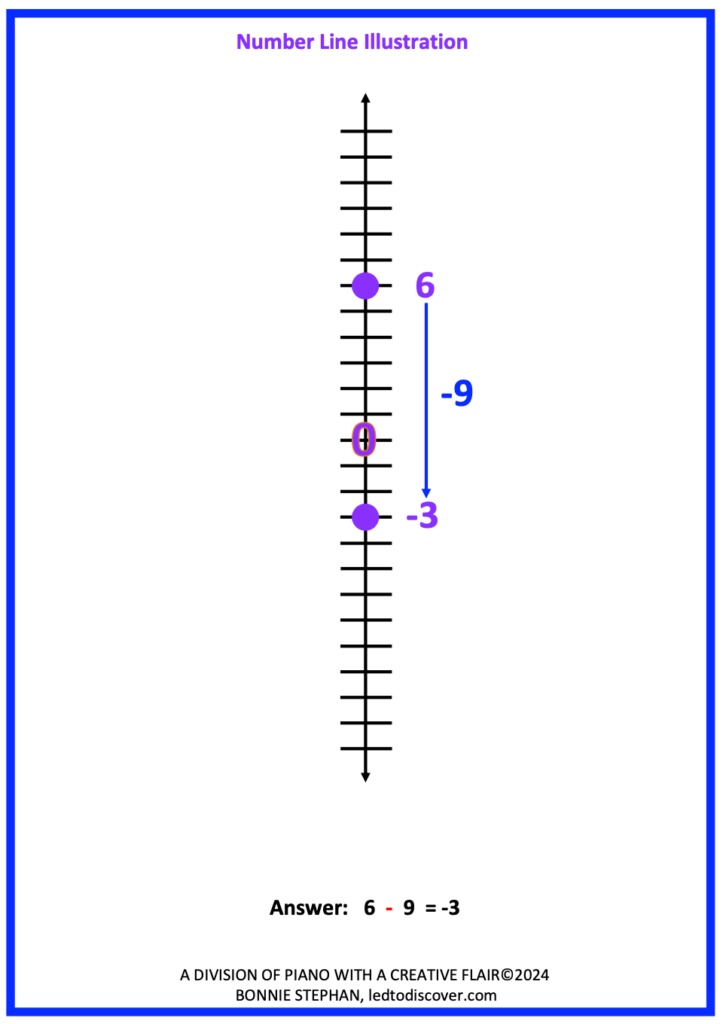
In the following problem, a horizontal line has been used for the money problem.

Conclusion:
Once students have experienced success with integers, student success with other expressions using order of operations and solving equations will follow.