Are your students puzzled by integers? Has this concept been challenging to explain? Have students struggled to grasp these new ideas? Keep reading to discover the best methods for introducing integers, negative and positive numbers, through strategies and games.

Contents:
- Introduction
- 1. What are Integers?
- 2. Number Lines
- A. Absolute Value
- B. Simple Operations with Integers
- 3. Class Activity
- . Number Talks: Integer Applications Related To Temperature and Money
- 4. Games
- Conclusion
1. What are Integers?

Simple examples using positive and negative signs help students see the connection between a negative and a positive number. See the examples below.


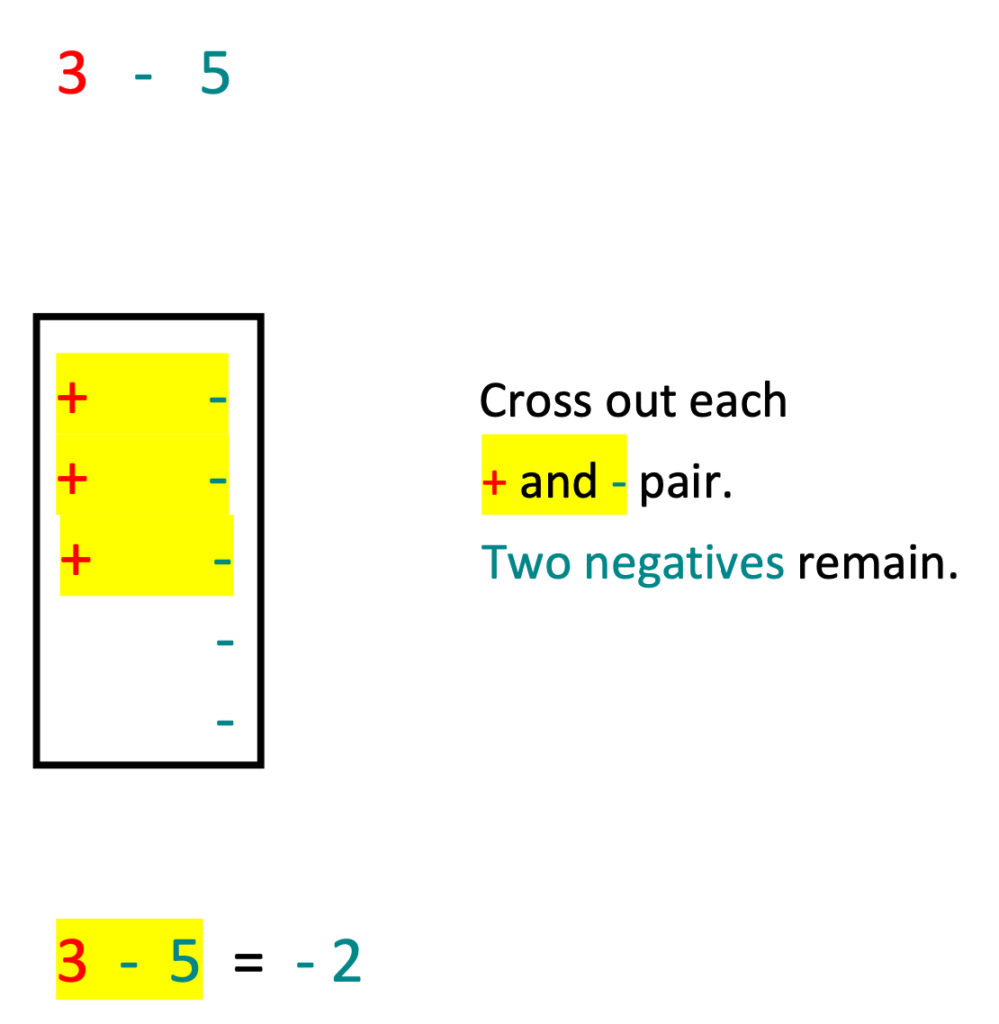
2. Number Lines

A. Absolute Value
Before introducing number lines, be sure students understand absolute value, the distance from a point and zero on the number line.
For example, in the number line below, the number of units between 0 and positive 5 is 5 units.
This holds true for numbers – 5 to zero which is also 5 units.
Even though the numbers to the left of zero are negative, the same number of units between
-5 and 0 illustrate a distance of 5 units.
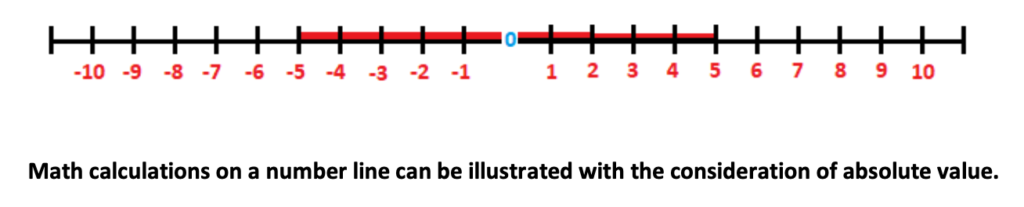
Absolute value is a common challenge in which students learn best through visualizing a number line. In turn, understanding absolute value further helps students understand the operations of integers.
B. Simple Operations with Integers
Math calculations on a number line can be illustrated with the consideration of absolute value. See the examples below.

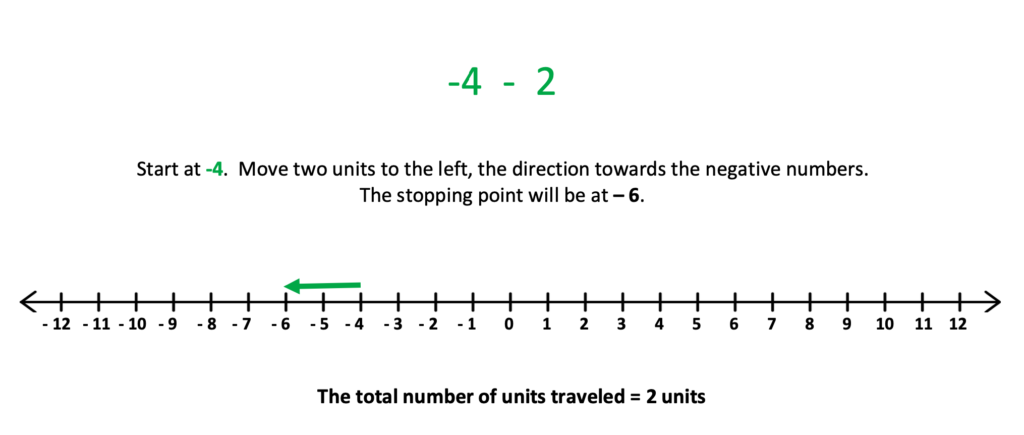
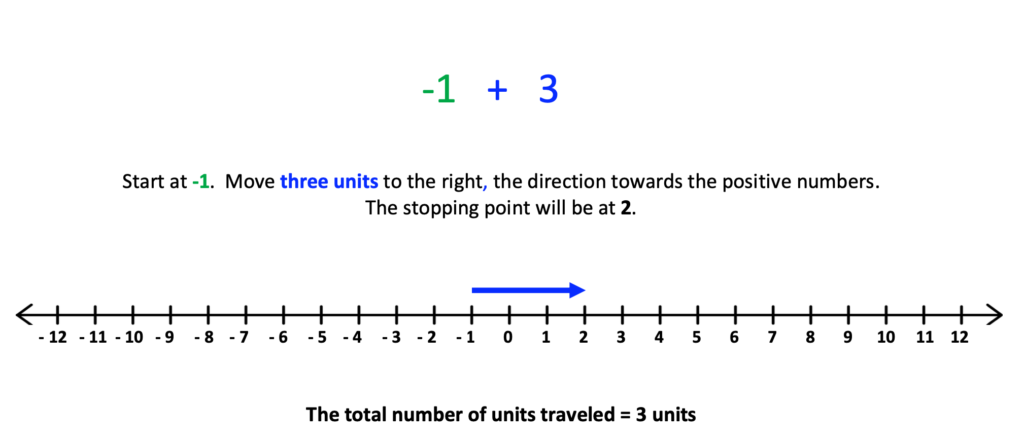
While discussing negative numbers on the number line, emphasize that though the numbers appear to increase in size when moving right to left from zero, the value of each number decreases.
To emphasize this concept, practice using in-equality signs to compare negative numbers.
See the examples below.

3. Class Activity
To get students up, and moving around, ask students to stand in a straight line. Now, ask them to walk forward two paces. Ask the approximate number of inches or centimeters they stepped forward.
Next, have the students return to their original starting position. Then ask them to walk backward two paces. Ask the approximate distance they step backward. Also, ask the students to walk two paces to the right and then to the left estimating the distance for each direction.
After the activity is completed, students will discover that no matter what direction they walk, distance will always be represented by a positive measurement.
4. Number Talks: Integer Applications Related To Temperature and Money
The beauty of integers is that they are a part of our everyday life. For example, the rise and fall of the temperature, money gain, and money loss are a couple of applications.
Often, even before introducing integers formally, I will take students on a simple journeys that goes something like this:
“Welcome to class! Today we are going to have fun with numbers. Clear your desk. Ready?”

Money conversations also provide much insight. See the examples below.



Below are other examples related to money gain or loss set up in column form.
In these examples, the terms, “negative experience” and “positive experience” I reference it to how I might feel if I lose money money or gain more money.
Also, words related to loss are in red, whereas words related to gain are in green.
In addition, the words with red and green also reference the answer to each question.

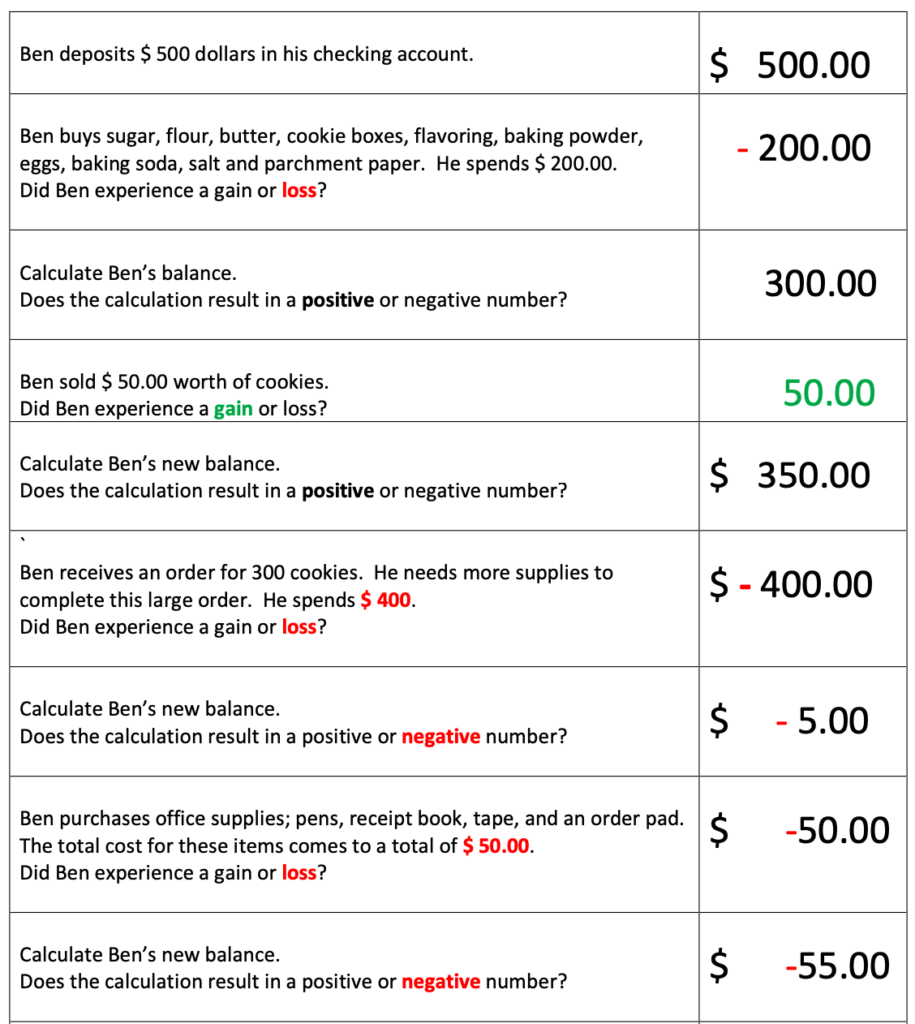
This next example references the use of simple applications that may be related to a checking account.
Ben wants to start a cookie business.
He lives at home with his parents and will make the cookies in his mother’s kitchen.
All the baking equipment Ben will need is in the kitchen.
Ben will need to buy ingredients to make his cookies. He may also purchase boxes to sell his cookies in. Other expenses may include business supplies.
Ben’s father gives him 500 dollars to establish his in-home business. Ben deposits 500.00 dollars in a checking account.
The calculations below are based on Ben’s money transactions.
4. Games
Number Line Dice Toss
What You Will Need
Dice: If dots are on the dice, include a negative for the sides 2, 3, and 5.
Also, add a positive sign to the same dice, representing sides 1, 4, and 6.
A large, styrofoam type of dice is great, though traditional dice are also effective.
White Board and Dry-Erase Markers
If a large enough whiteboard is not available, place labeled sticky notes evenly spaced, in a straight line on the
floor or across a wall.
When using sticky notes, the number line can be designed either vertically or horizontally when placed
on the floor.
Outdoor Option:
If allowed, draw the number line on the pavement using chalk.
Set Up
Involve students as much as possible in setting up the game.
White Board:
Draw a number line on a whiteboard, from – 10 to + 10. Allow space for students to stand at least 6 inches apart from each other.
Sticky Notes:
Write a single number on each sticky note, starting at – 10 to + 10. Place notes on the floor in a straight line. Allow space for all students to stand at least 6 inches apart from each other.
How to Play the Game
Starting Position
All students start, standing in a line in front of zero. Each student takes a turn tossing the dice and moves according to the sign and number on the dice
For example:
If a – 3 is tossed, the student moves 3 units to the left.
If a + 4 is tossed, the student moves 4 units to the right.
The student remains in that position until their next turn, then tosses the dice again and moves according to the number and sign. If a student moves past -10 or +10, the student is out of the game.
The Winner: the last student standing “in the number line” between -10 and +10.
Dig for the Gold!!!

DIG FOR THE GOLD!!!
What you will need:
- Six-sided cube, numbered 1, 2, and 3
Smaller numbers make the game last longer and provide for easy calculations. - Six-sided cube
Label four sides with negative signs. Label the remaining two sides with positive signs. - One game piece to represent each player
If there are no game pieces, creativity is encouraged; pencil erasers, buttons, paper clips, water bottle caps, Legos, etc.
Directions:
- The player places the game piece at the START, -1. The player tosses both the number cube and the sign cube.
- Round 1:
If the player tosses a positive sign, the player must wait till the next round to play, to roll a negative number.
If the player tosses a negative sign, the player moves down the number of rows according to the number tossed.
For example, if a negative cube and the number 4 is rolled, the player would move the game piece from – 1 down to
–5.
2. The Following Rounds: each player continues to take turns until reaching the pot of gold at the bottom of the page. If the player rolls a positive sign, the game piece must be moved that number of times up the page.
If the player moves up to the START position or moves past the START position, the player will need to wait till the next turn to roll for a negative number to begin moving back down the page.
For example, if the player is on -2 and rolls a + 3, the player would go past the – 1 position.
3. The first player to cross over – 16, wins.
Conclusion
Though certain students will make sense of certain strategies more than others, you now have options. Now you have strategies, methods, and games! And yes, it can be fun! You’ve got this!
Click the above link to find 3 Games and a Word List for Integers

