Do students understand how to simplify rational expressions with opposite signs? Keep reading to discover strategies for success.
#1 – Simplifying Fractions
First, introduce students to what they are familiar with. Start with what they know before adding new elements of greater complexity. Providing a review will decrease the number of times students ask questions related to basic fraction operations when solving rational expressions.
For example, I begin with a simple problem such as 5/10. See the examples below.
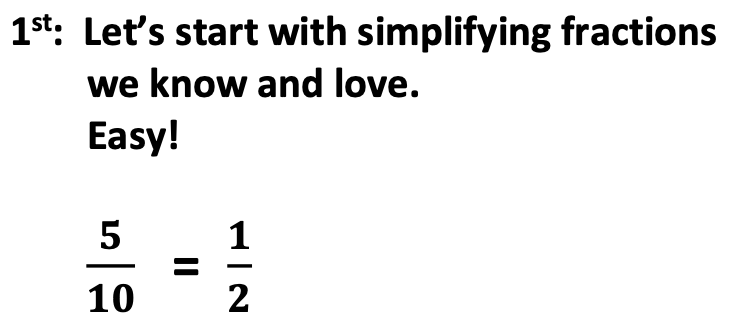
In addition, include a fraction that reduces to a number over 1.

#2 – Simplifying Fractions with Integers
Next, you are hoping that students remember integer rules. On the other hand, I include this concept just to be thorough.
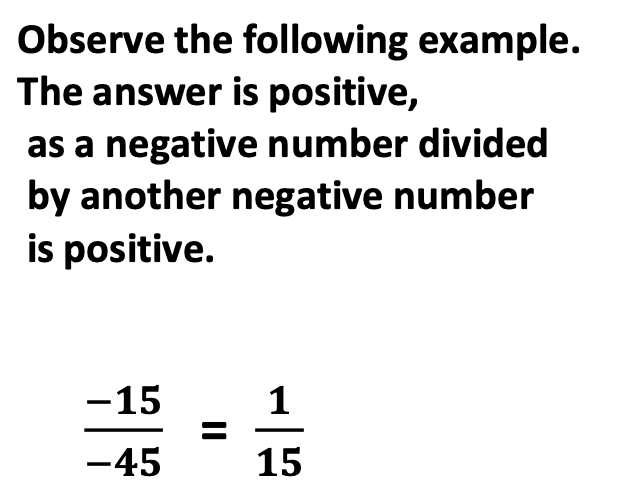
Again, emphasize the equivalent value of each answer, regardless of the location of the negative sign. Students often forget this.
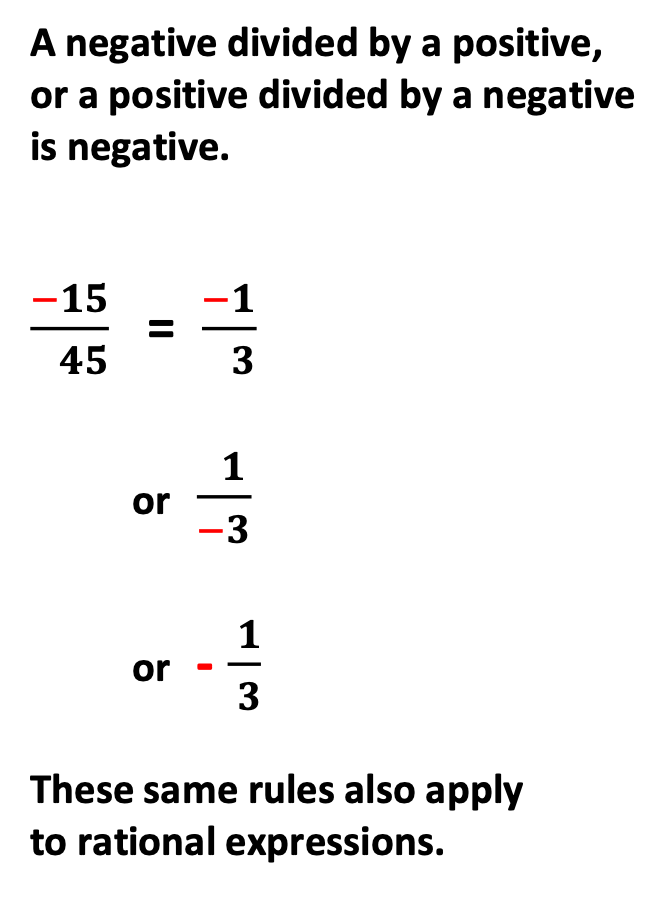
#3 – Rational Expressions Equivalent to One
Furthermore, remind students that a set of positive terms divided by the same set of positive terms is one, not zero. During review, emphasize this by using a simple illustration as given below.

For example, I notice this error with problems like the one below. When students slash through the top and bottom of the expression, they assume that the answer is zero. Emphasize the invisible 1 in front of each.
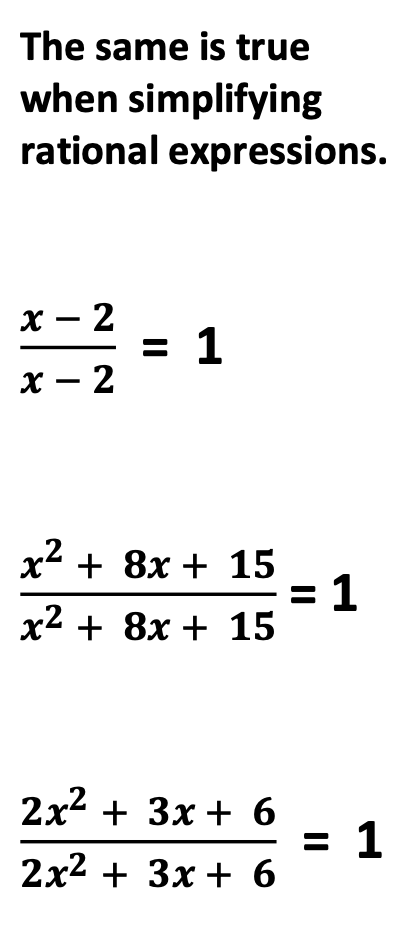
Understanding these concepts is paramount.
#4 – Solving Opposite Rational Expressions
A. Opposites
Next, provide simple examples with opposite signs. See the example below

Also, notice the color-coding of numbers and signs. Visual learners and those with visual challenges will find color-coding significantly helpful.

Likewise, line up like variables and numbers.

Then, factor out a negative 1.
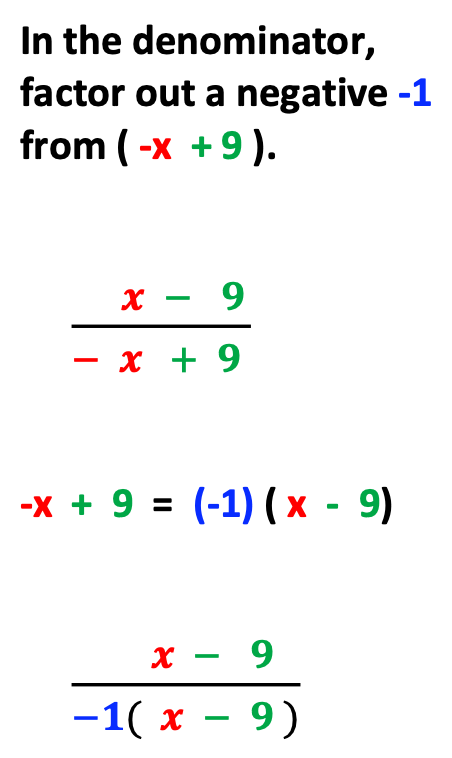
Next, explain to students why this works.

Now, students see it can be further simplified.

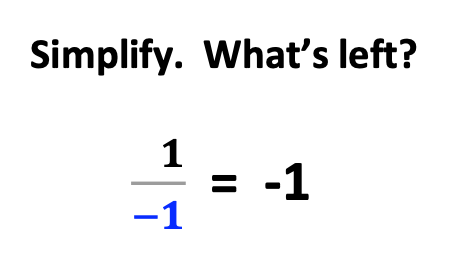
B. Another Example: Rational Expressions with Opposite Signs
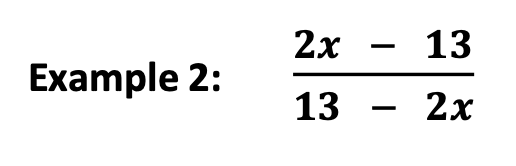
Next, provide another example that includes the same steps.

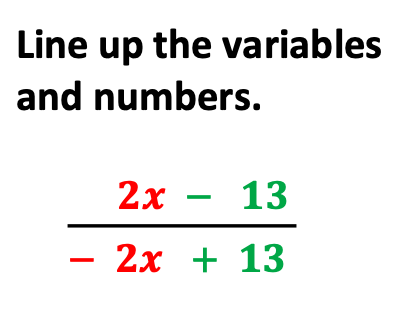


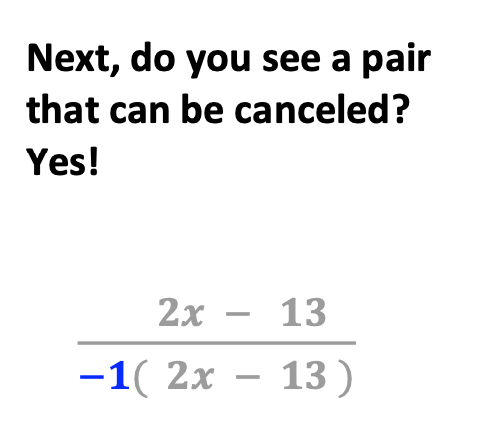
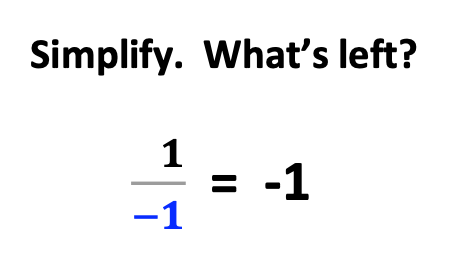
B. Factor First! Binomial
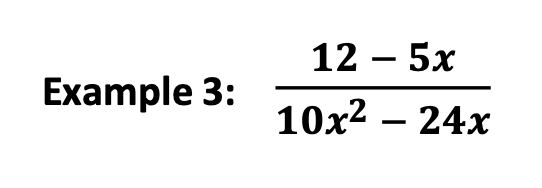
Now illustrate a binomial with a GCF. Then follow the steps as described in the previous examples.
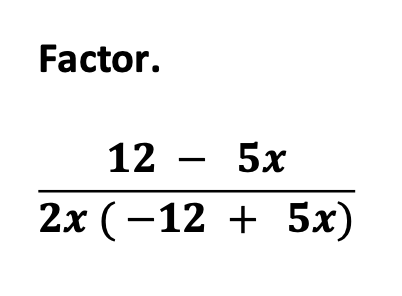
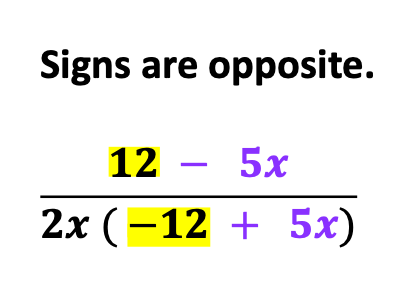

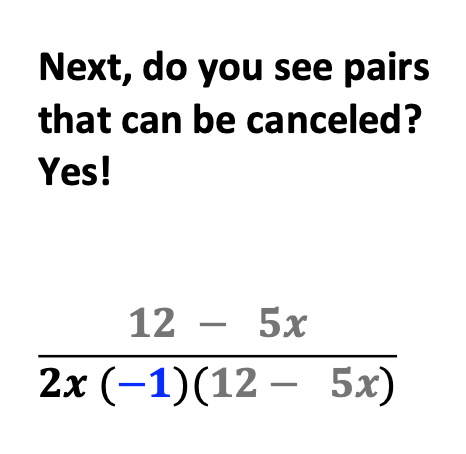
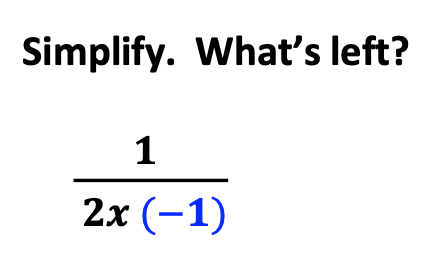
C. Factor the Trinomial
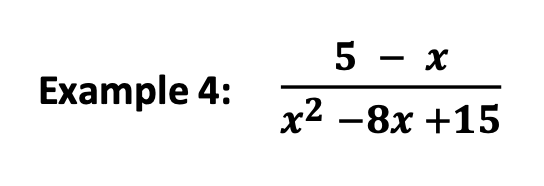
Next, provide this example that includes a trinomial that may be factored.
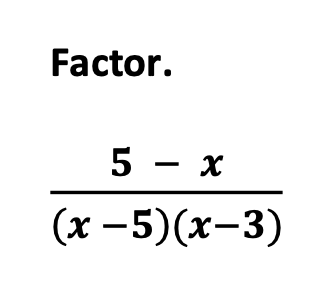
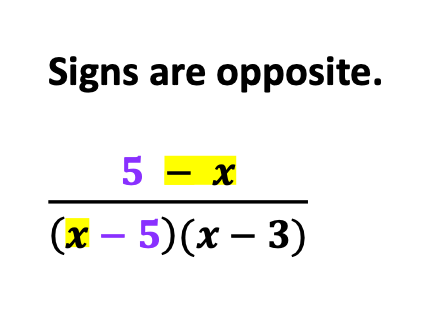
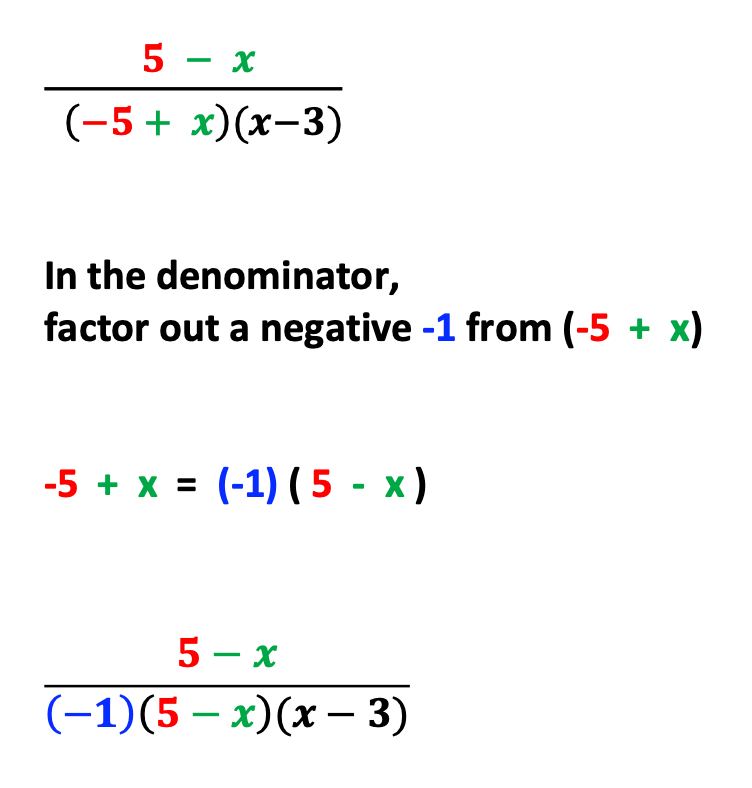
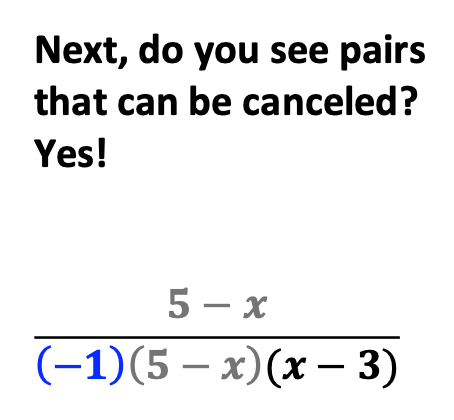
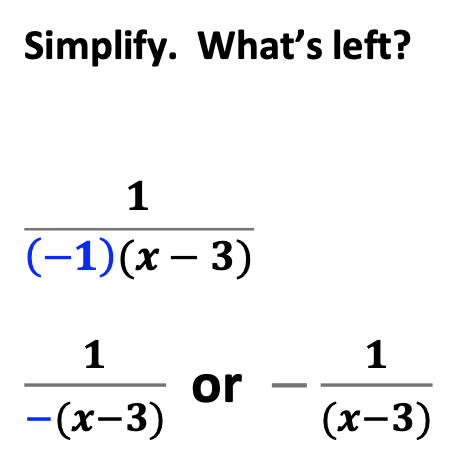
Conclusion
In conclusion, start what is known. Add one new concept at a time. Use color-coding. This represents a recipe for success!
Other Related Posts
A Related Resource
How to Find the Domain of Rational Expressions
Looking for More Materials?
Click the button below to view more of my educational resources!
