Looking for a quick and easy way to explain how to simplify radicals? Wondering where to start? As you continue reading you will discover how to prepare to successfully simplify radicals.
#1 – Prepare to Simplify Radicals
Before simplifying radicals, prior knowledge in the following topics provides student success. These topics include divisibility rules, factors of numbers, and square root values. When students present with a solid understanding of these skills, students make a smooth transition to simplifying radicals.
#2 – Divisibility, Factors, and Square Roots
Next, observe strategies that will prepare students.
A. Divisibility Rules
Students often remember that even numbers are divisible by two. They may also recognize that a number ending in zero is divisible by five and ten. On the other hand, they are often unfamiliar with numbers divisible by three, six, and nine. This concept may be most effectively reviewed starting with a divisibility reference sheet that lists divisibility rules.
Below is an example of a page with divisibility rules.
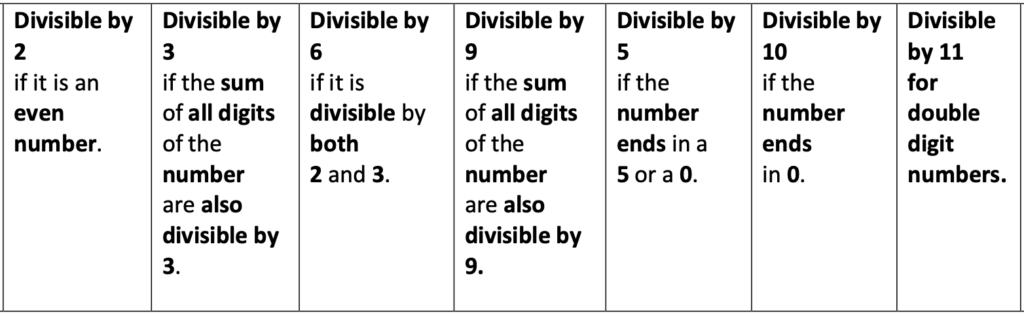
After students understand each rule, they are ready to use the rules to list the factors of numbers.
B. Factoring Numbers
When students are confident with divisibility rules, they can factor numbers at a much faster rate. Below is an example of listed factor pairs for 48.

Notice that the factor pairs are listed vertically. Numbers on the left are discovered when using the divisibility rules. To complete the factor pair, students may consider math facts they know, such as 6 x 8 and 4 x 12. Factors for even numbers can be easily listed by breaking 48 in half.
My students are always impressed with this method when factoring both small and large numbers.
Next, provide students with practice writing factors for numbers 12 – 100. Remind students to use divisibility rules. Start with even numbers such as forty-eight. Next include “money” numbers such as 50, 75, and 125.
For more strategies and details for divisibility rules and factoring, see the following resources at:
https://www.teacherspayteachers.com/Store/Bonnie-Stephan

C. Square Roots
Preparing to simplify radicals is like making your favorite layered food like a cheese pizza. Place the dough on the pan, cover the dough with sauce, and sprinkle with cheese on top. When simplifying radicals, divisibility of numbers is the dough, factoring numbers is the sauce, and finally, square roots are the cheese! And what is pizza without cheese where I live? Not a pizza.
So, yes. The ability to identify and simplify perfect square numbers is also an important of the process of simplifying radicals.
Some square roots include hints. For example, the square root of zero is zero. The square root of one is one. Sometimes the square root includes an answer within its digits. For example, the square root for 36, is 6.
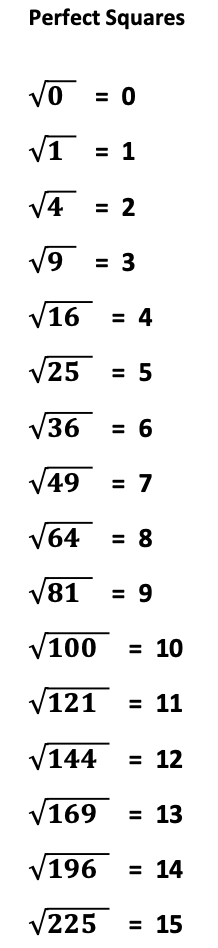
For more on square roots, you may be interested in the post,
Exponents in Pre-Algebra: How to Easily Explain.
Click on the link below
Exponents in Pre-Algebra: How to Easily Explain
#3 – Roots? Radicals?
Roots? Radicals? What is the difference? Students may notice that these terms are used interchangeably.
The terms “root” and “radical” are both used in the example below.
Notice that the terms “square root sign” and “radical sign” can both be used to describe the same thing.

Later, students will be introduced to cube roots. The same basic sign is used, though a small three will be found in the “v” portion of the sign. Though the symbol may still be referred to as a root sign, it will also be identified as the “cube root” sign.
#4 – Steps to Simplify Radicals: An Example
Now students are ready to learn the steps for simplifying the radical.
Share that the first step will require students to list factor pairs for the number 32. Next, explain that factored pairs with a number representing a perfect square may be circled.

Once the perfect square number is identified, the largest perfect square is chosen.

Next, simplify by taking the square root of 16, which is four and place it outside the radical sign.
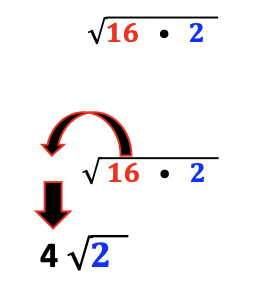
Since 2 cannot be simplified, it will remain within the radical sign.
Conclusion
Success in simplifying radicals requires the ability to list factors of numbers. Listing factors of numbers is easiest when students know divisibility rules. Students can confidently complete steps for simplifying radicals when they identify numbers representing perfect squares.
Looking for the perfect resources for student practice? I’ve got you covered. See resource options below.



One of the resources is FREE!
Click on the blue link below to learn more.
Looking for More Materials?
Click the button below to view more of my educational resources!
