Are students struggling with square and cube roots? No problem. Keep reading to discover fun, easy, and interesting strategies.
#1 – Introduction to Square and Cube Roots: My Favorites!
I love teaching square and cube roots! They are beyond beautiful! Before you are finished reading this post you will discover fascinating patterns!
Square and cube roots are introduced in middle school and applied in order of operation problems. Later in algebra, square, cube, and other roots are applied in more complex algebra problems. This is just another reason to appreciate square and cube roots.
#2 – Understand the Anatomy
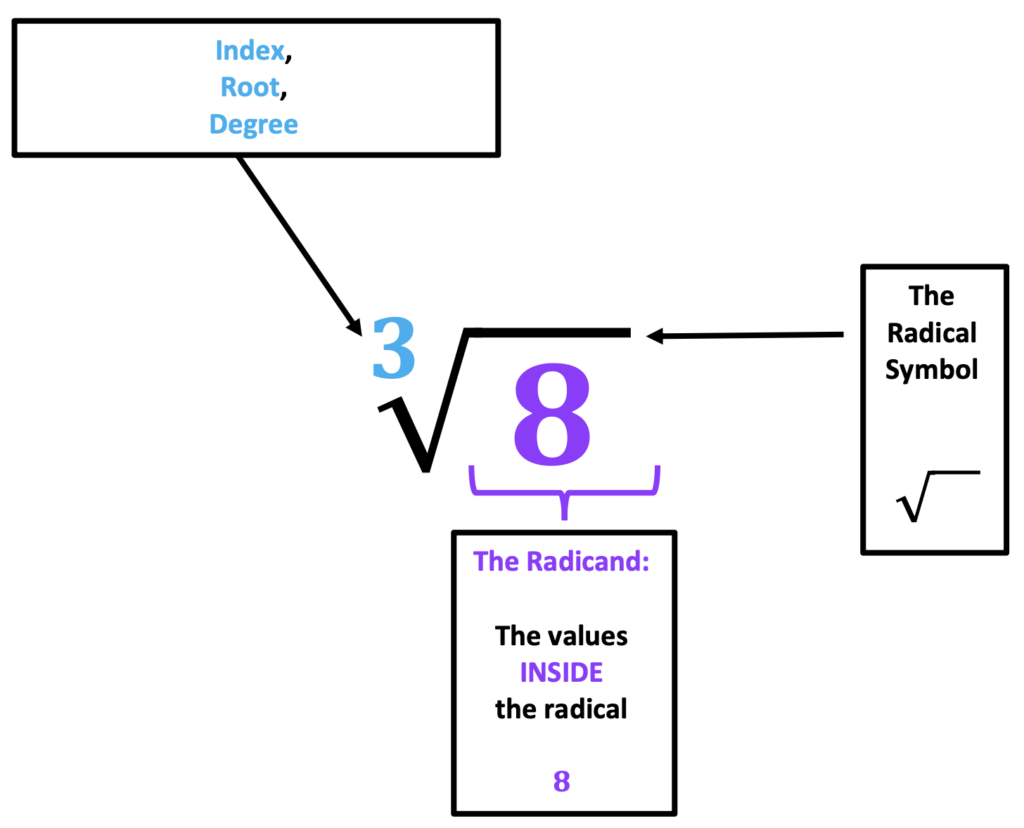
Understanding the “anatomy” of roots is important as students commonly identify the design of a square root symbol to represent the symbol for long division.
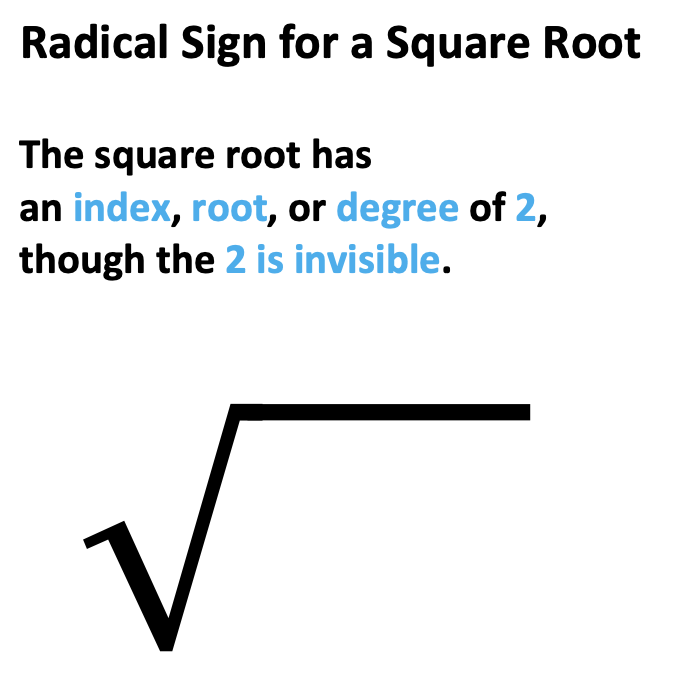
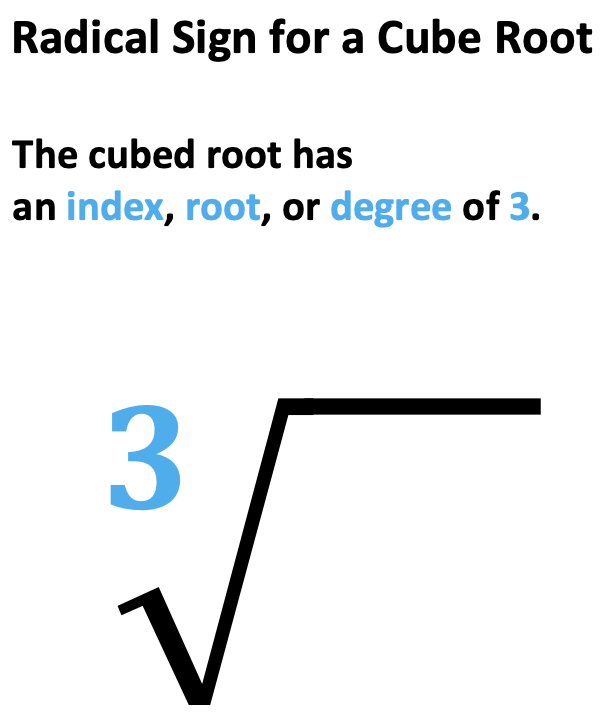
When observing root signs three and larger, you will see a specific number listed beside the root sign located inside the v-shaped part of the sign. This number may be referred to using any of the three terms: “Index,” “Root,” or “Degree”. For example, if there is a cubed root, it will have the number 3, as illustrated below. On the other hand, it is important to note that the square root sign does not include a written two within the v-shaped part of the sign.
Observe the illustrations below.
Square Root
CUBE ROOT
Anatomy of a Root

#3 – Patterns for Square and Cube Roots
Furthermore, there is nothing more fun than discovering the obvious. Maybe you are familiar with the saying,
“The answer is right in front of you!”
The following examples will demonstrate this concept.
A. Square Roots
As you scan the list below, notice the answer is inside each sign. For example, the square root for 36 is 6.
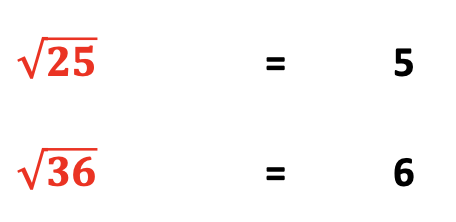
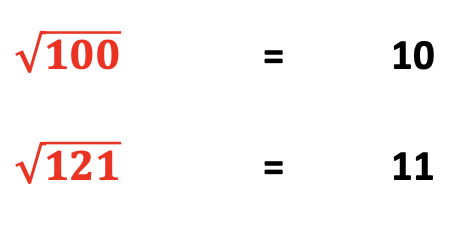
The square root for 121 is 11.
Another fascinating characteristic of 121: the outside numbers, ones, when added together equal the digit of the inside number, two.
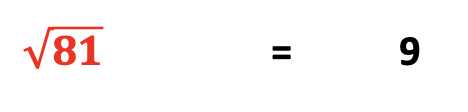
When the digits 8 and 1 are added together, the result is 9, yet another interesting pattern.
B. Cube Roots
Likewise, just as the answers for square roots are found within the square root, the answer may also be found in cube roots.

Though the answer for the cube root of 512 does not include a number representing the answer, observe what happens when the digits are added together. 5 + 1 + 2 = 8
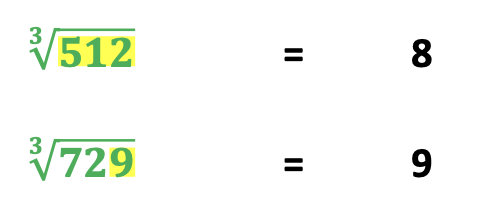
The cube root of 729 shouts from the mountaintops, “Nine!” First, notice that the answer is in the problem. Second, notice what happens when the first two digits are added together: 7 + 2 = 9. Third, the first two digits, 72 also bring to mind the multiplication fact, 8 x 9 = 72.

Also, note that the cube root of 1331 is 11. First, as in the square root of 121 = 11, the cube root of 1331 is also 11. Second, let’s look at another fun fact. The cube root of 1331 is the result of: 11 x 11 x 11 = 1331. How many times was 11 multiplied? Three! What are the numbers in the middle? Three!
#4 – A Sneak Peak at Simplifying Roots in Algebra
Furthermore, these concepts are applied later in Algebra. We will take a quick look at what is referred to as, “Simplifying the Radical”. I refer to this process as: “Break it up. Take it out.”
The process is quite simple.
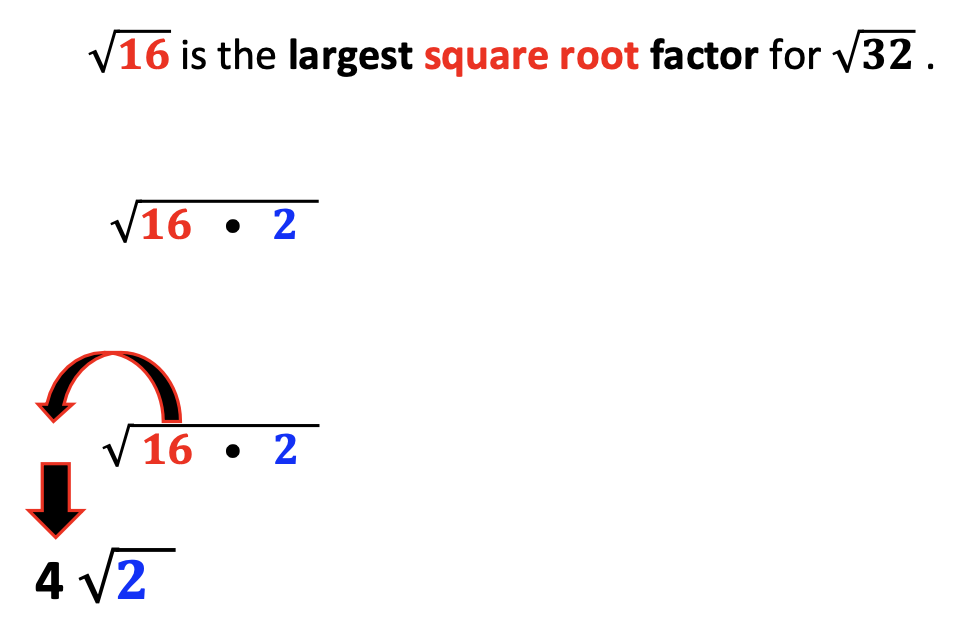
1. List the factors of the number.
2. Identify the LARGEST factor. In the example below, the number is 16.
3. Select the factor pair with the largest factor, 2 and 16.
4. Take out the square root of 16 which is 4.
5. Two remains inside, as it is not a perfect square.

Conclusion
Square and cube roots are easier to memorize when parts and patterns of each are identified.
Looking for student resources on this topic? Select the “Learn More” button at the bottom of the page.
If you found this post interesting, you may also enjoy: “9 of the Most Important Middle School Math Concepts to Know Before Pre-Algebra”.
Looking for More Materials?
Click the button below to view more of my educational resources!
