Multiplication Facts: How to Build Problem Solving Skills

Do your students struggle with multiplication facts? Maybe you have tried flashcards, games, and worksheets, yet they continue to struggle? What strategy do you use when a student asks you what 7 x 6 is? Do you quickly answer? Or, do you use a strategy that the student can use independently? Are you familiar with methods that help students develop an awareness of number patterns? Continue reading to discover solutions for building student independence and problem-solving skills.

Multiplication Facts:
“Start with What You Know!”

Zero Trick with Big Numbers

First, to create a positive learning experience with multiplication facts, start with what the student knows. This is significant, as what is known provides a link to apply new information, one small step at a time. For example, start with small numbers and then gradually include other numbers.

For example, let’s start with numbers that are multiplied by numbers with zero. Begin with 6 x 1. Next, 6 x 10. As you illustrate, ask students to write down any observations they notice. Afterwards, encourage students to share their observations and then create their own examples.

multiplication facts: numbers with zeros

Notice how the final answer includes the number and the number of zeros. Once students recognize this concept, they can approach these problems confidently. They are no longer fearful of the number size. Color-coding helps students quickly see the relationship of zeros and other numbers multiplied.

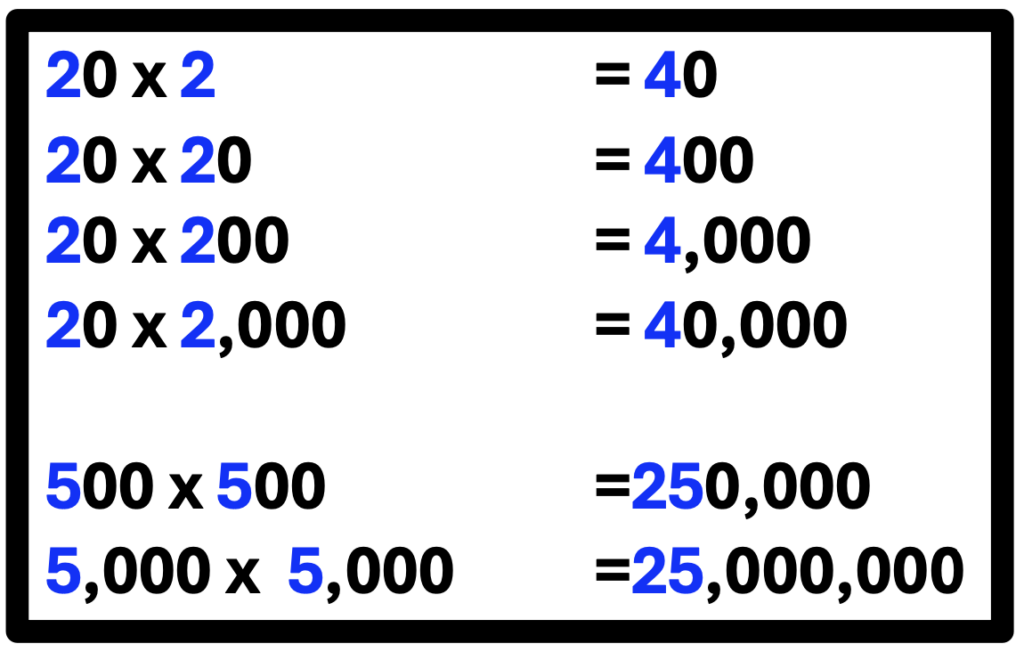
Furthermore, though most students learn multiplication facts with numbers, 2, 3, 4, 5, 10, and sometimes 9, the facts with 6, 7, and 8 can be the most challenging. As teachers, it is not unusual to think, “Well, at least they know the others,” as we hope they will somehow memorize these over time.

Likewise, if you teach high school math, you know there are students who use a calculator to determine basic multiplication facts. The most common include mutliplication with 6, 7 and 8. The following are ways to address 6, 7, and 8.

Tricky 6

Start with what students know. We will also help students recognize patterns.

Tricky 7

Next, like the 6’s, we will start with what students know and integrate pattern concepts. The most common 7 facts include 7 x 4, 7 x 6, and 7 x 8.

Tricky 8

Furthermore, we will repeat the strategy by starting with what is known and helping students recognize patterns.

Conclusion

In conclusion, when students start with what they know they are able to create pathways that lead to answers. The examples illustrate how students can use these discoveries to independently problem solve. This process also increases student number sense which promotes success with future calulations.