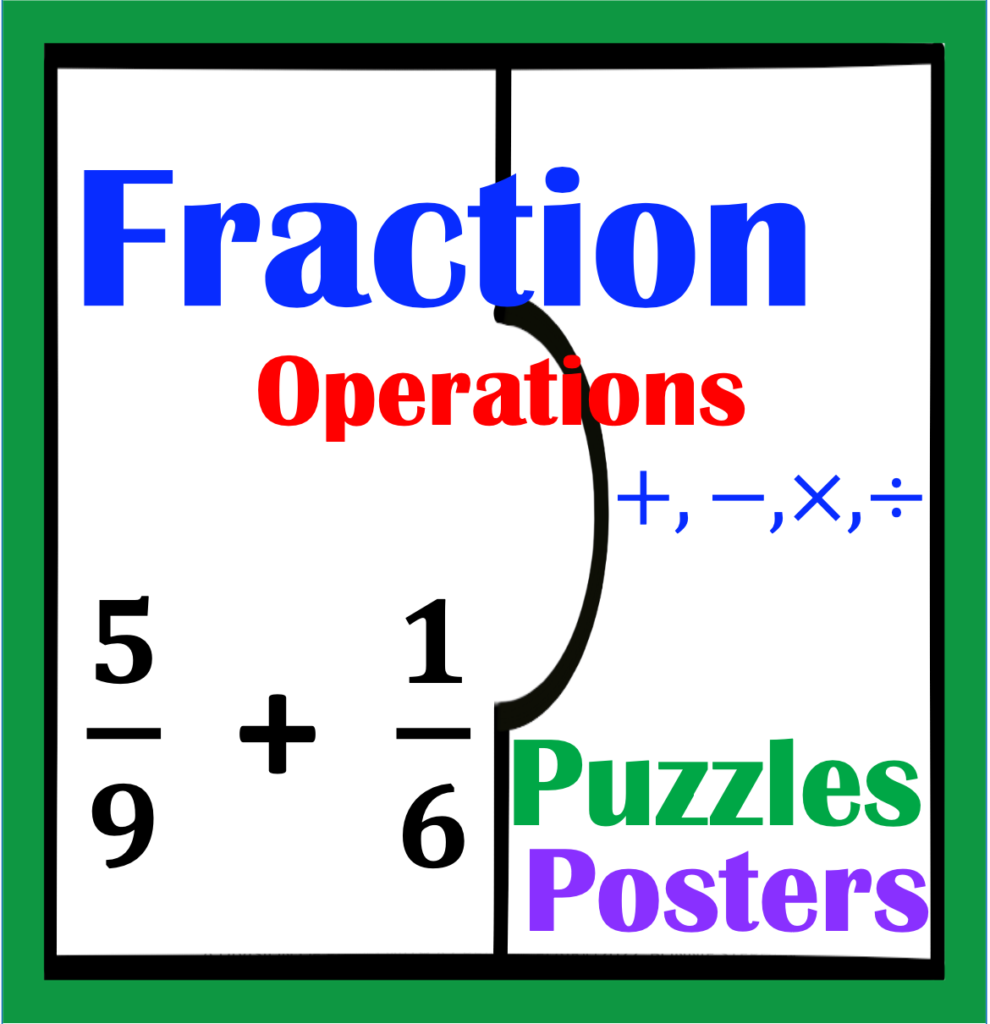
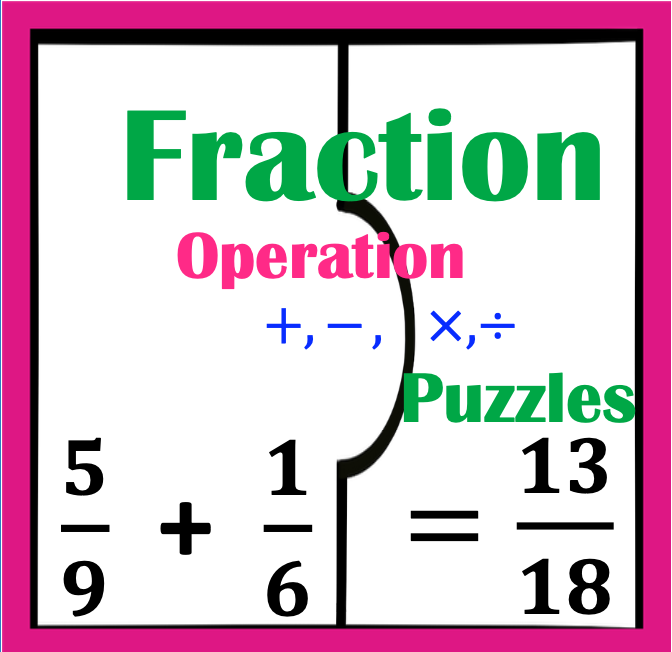
Looking for a successful way to teach students how to plot points on the Cartesian Plane? Dreading student confusion that can come with this topic? Dread, no more. Keep reading to discover strategies to meet student needs.
- Introduction
- 1. Review the Cartesian Plane
- A. The Big Picture: Quadrants, Zero, the X and Y Axis
- B. The X and Y Axis and the Origin
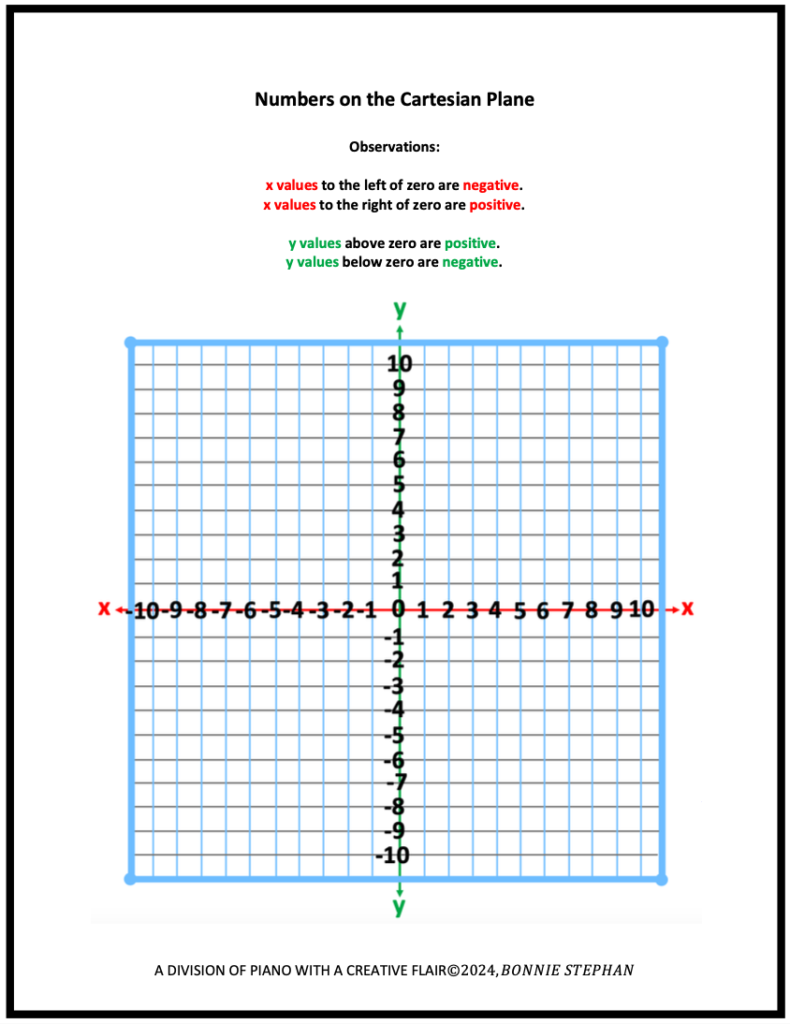
- C. Numbers on the Cartesian Plane
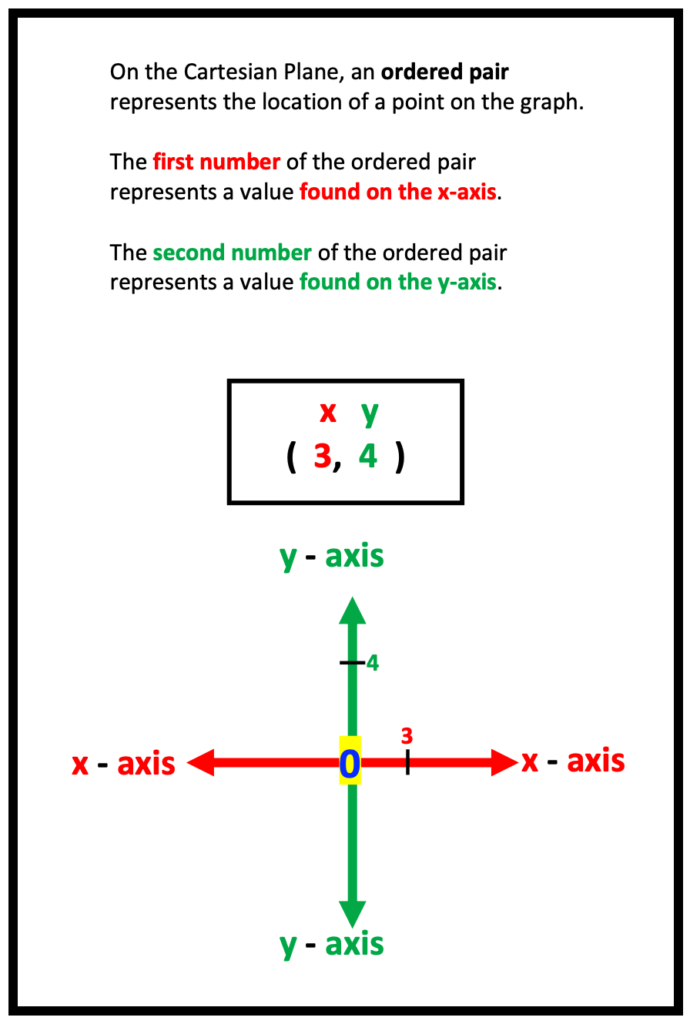
- 2. Define and Illustrate the Ordered Pair
- 3. Practice Plotting the Ordered Pair
A. Method 1: Sketch
B. Method 2: Cartesian Plane
C. Other Points of Interest
Conclusion
1. Review the Cartesian Plane
If you have not done this already, be sure to provide a review of the Cartesian Plane. Point out the origin, quadrants, and the x and y axis, Also, point out that each axis includes 0, negative and positive numbers. Below are three illustrations.
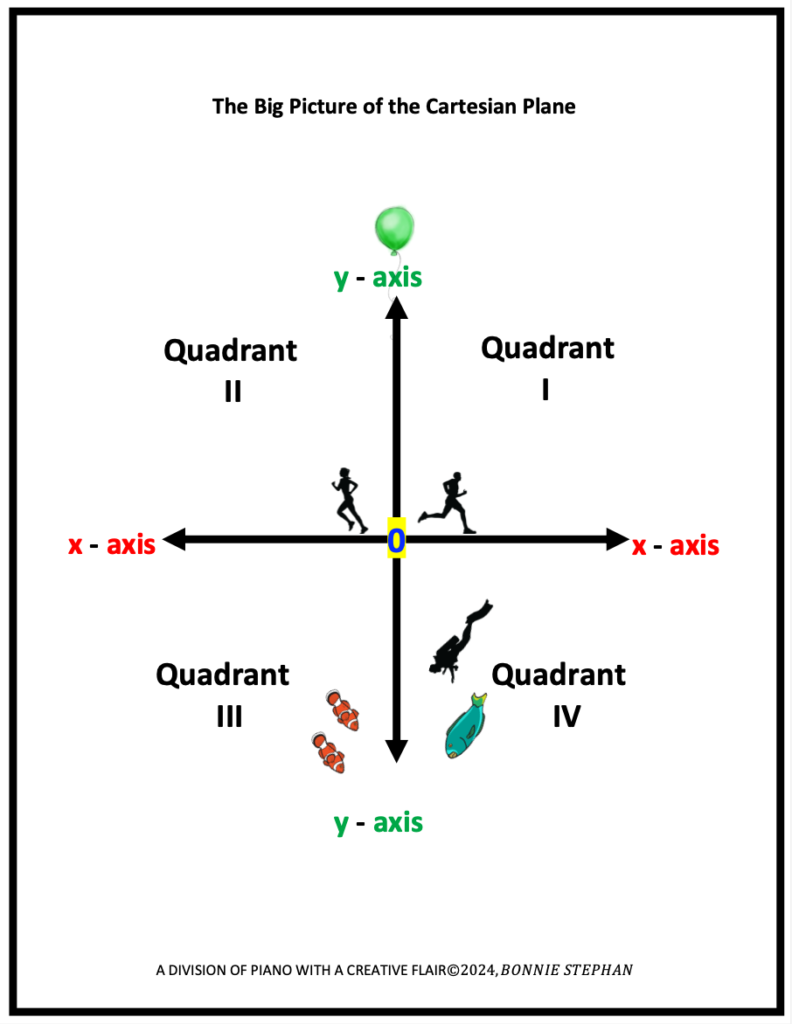
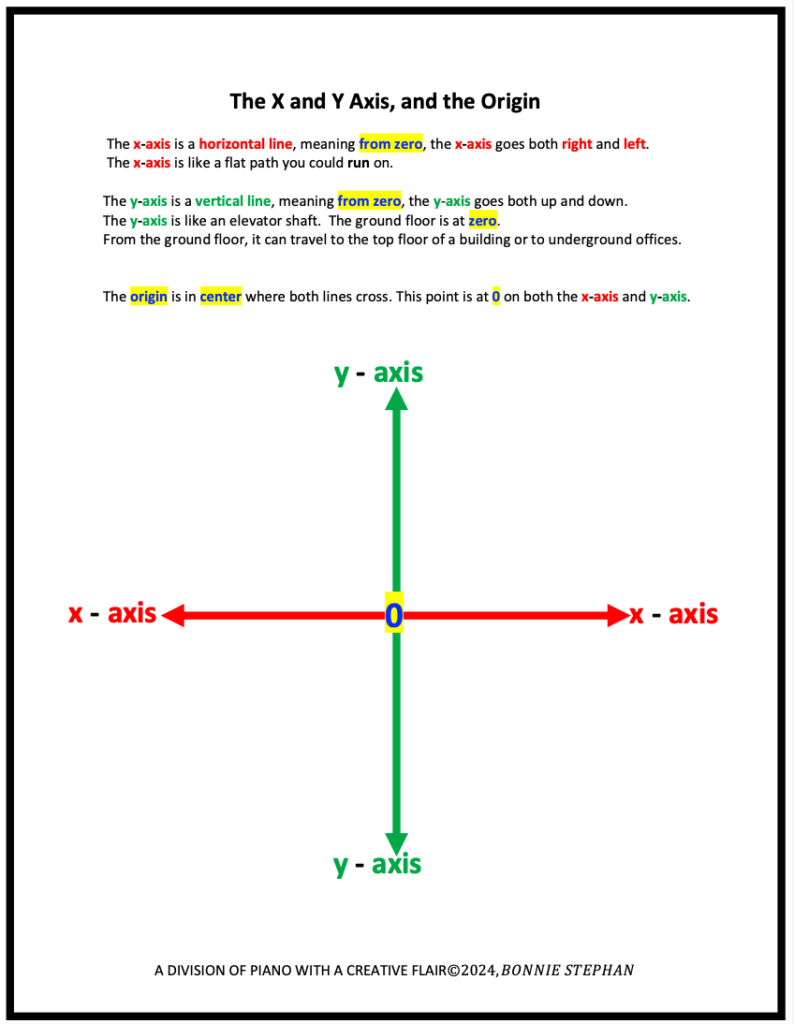
2. Define and Illustrate the Ordered Pair
Next, help students visualize how the ordered pair relates to numbers on the x and y-axis. Note that the use of red for the x-axis, and green for the y axis is a theme carried over from the two illustrations prior. By providing a color theme for x and y, students are able to easily make connections from one graphing concept to the next.
I have found that the use of consistent colors is very helpful not only with plotting points, but with other math concepts that commonly follow in which x and y are also used. Examples include using formulas to find the midpoint or determining the distance of a line segment.
3. Practice Plotting the Ordered Pair
A. Method 1: Sketch, Run, and Dive, No Cartesian Plane
This method works well for students who are easily visually overwhelmed or directionally challenged and also includes learning through movement. When using the color theme such as red for x and green for y, the activity also adds a significant visual impact. The directions are as follows:
The teacher illustrates the meaning of an ordered pair by writing on a board or other tool that allows students to follow along. Students will need a ruler and may work in pairs.
While the teacher sketches each part, the teacher may instruct students to do the following:
“Draw zero. From zero, using a red pencil, run 3 inches to the right. Next, from the end of the red line, use a green pencil and dive 4 inches down.”
Student Participation Options:
1. Students “draw” in the air as the teacher sketches.
2. Students sketch on a white board as the teacher sketches.
3. Students sketch on paper as the teacher sketches.
B. Method 2: Cartesian Plane
Following this visual, kinesthetic (with movement) task, students will be ready to apply these directional concepts with greater confidence when plotting points on the Cartesian Plane.
In each sketched illustrations below, the word, “units” is used. For Method 1: teachers may choose the units they wish their students to use; inches, centimeters, etc. The actual use of the word, “units” will be more applicable when graphing points on the Cartesian Plane.
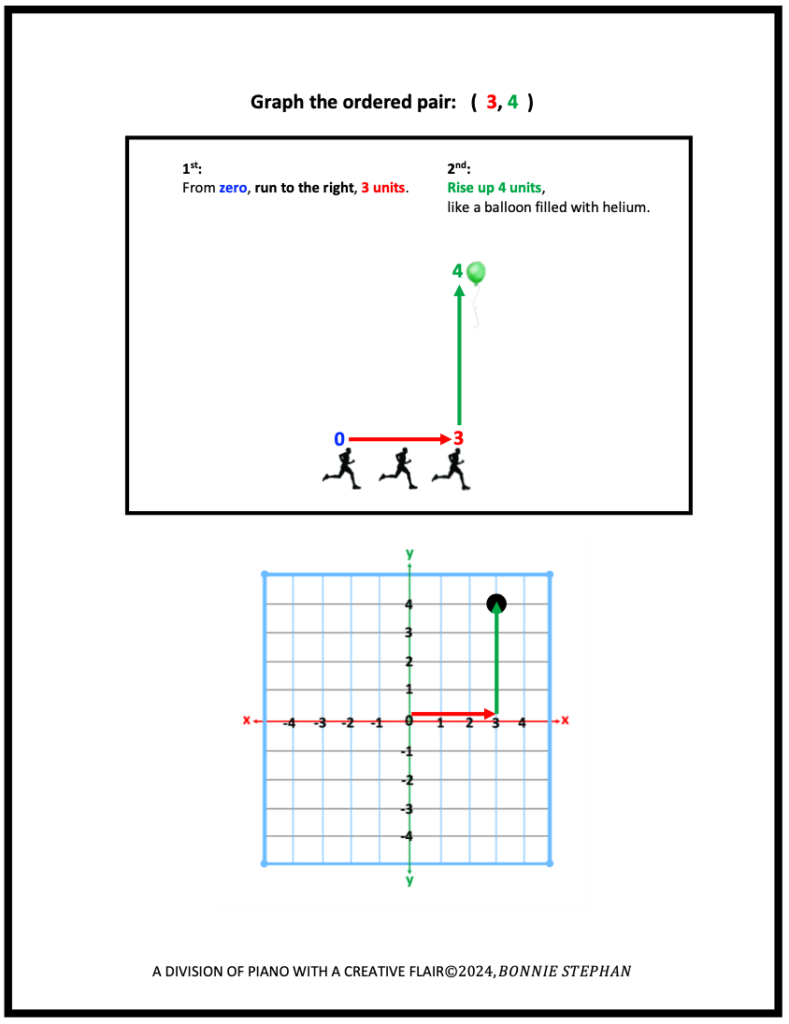
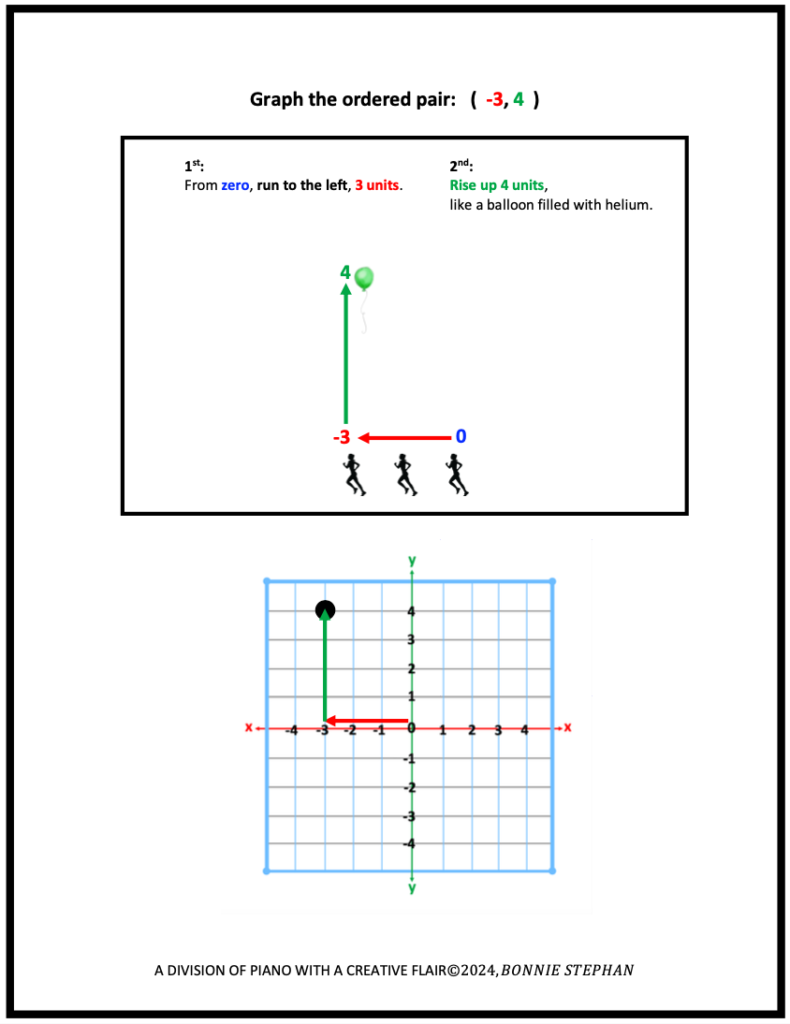
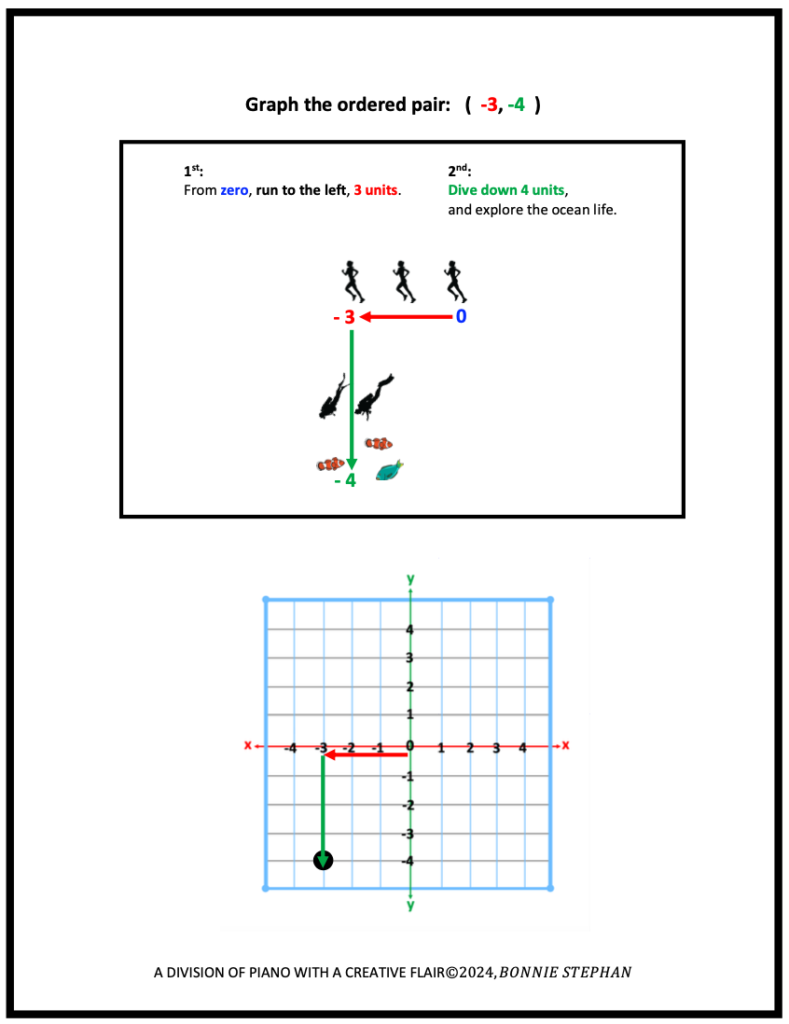
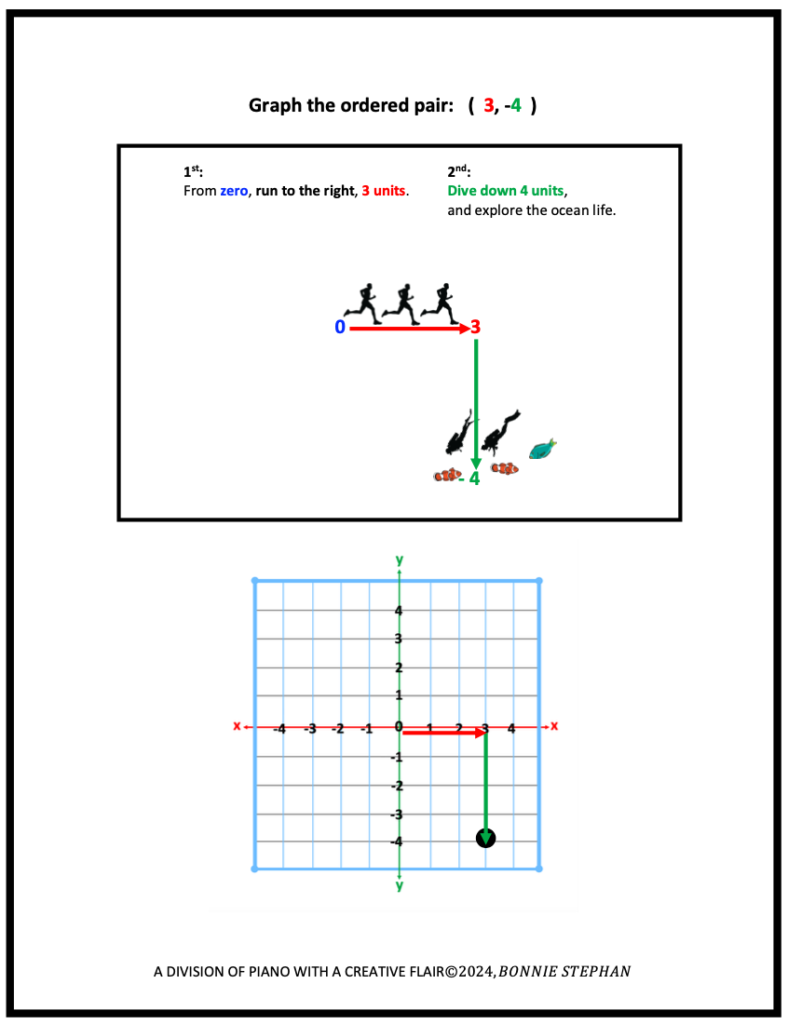
C. Points of Special Interest
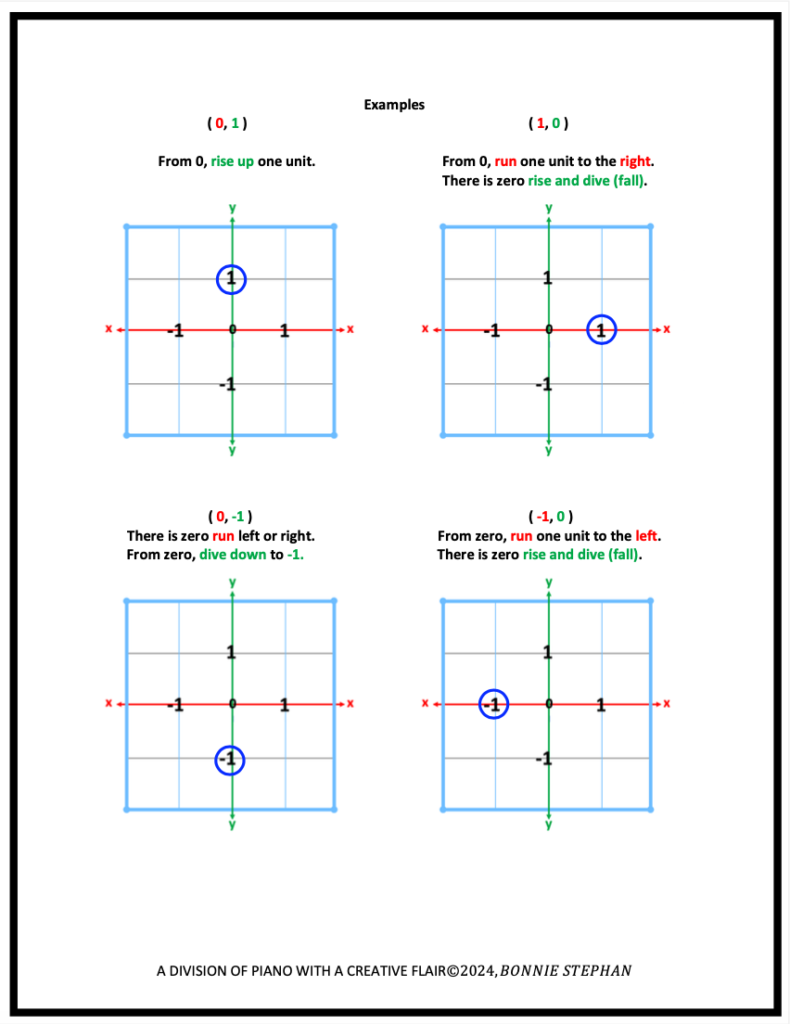
Certain points tend to be more challenging to graph than others. Those special points include ordered pairs that include zero.
For example, in the ordered pair, (0, 1), students are accustomed to moving to the right or left for the x value. In this case, zero is the x value on the x-axis. This being the case, the only move remaining is to rise up.
In the ordered pair (1, 0), students are quite comfortable traveling from 0 to 1 on the x-axis, though become quite anxious about where to go for y when the value is zero. Once again, like the previous example, y is already at 0, meaning that there will be zero movement to rise up or to dive down. The remaining illustrations are similar.
With practice, students become confident in graphing these types of points.
These are points that include 0.
Examples
Conclusion
When students are familiar with the parts of the Cartesian Plane, they are ready to begin graphing points. Though some students may be familiar with this concept, others may find these concepts visually challenging. By providing visual themes and kinesthetic (movement) activities, students will be successful in graphing points on the Cartesian Plane.