- CONTENTS:
- Where to Start in Middle School: Math to Know Before Pre-Algebra
- 1. Basic Math Operations in Middle School
- What middle school students need to know before pre-algebra
- 2. Listing Factors in Middle School: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- 3. Divisibility Rules in Middle School: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- 4. The Greatest Common Factor in Middle School: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- 5. Fractions in Middle School: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- Proper Fractions, Improper Fractions and Mixed Numbers: What are They?
- Converting Between Improper Fractions and Mixed Numbers
- The Least Common Multiple
- What middle school students need to know before pre-algebra
- 6. Decimals in Middle School: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- Understanding Place Value
- Comparing and Contrasting Decimal Values
- Rounding Numbers
- What middle school students need to know before pre-algebra
- 7. Percent in Middle School: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- Examples of Fraction, Decimal and Percent Applications from MiddleSchool to High School
- 8. Math Applications with Life Skills: Math to Know Before Pre-Algebra
- What middle school students need to know before pre-algebra
- 9. College Prep Testing
- 1. Basic Math Operations in Middle School
What do middle school math students need to know before pre-Algebra?
Are you overwhelmed by all the content taught in middle school?
Looking for specific concepts students need to learn before Pre-Algebra?
Throughout my teaching career over the past 17 years, I have observed that students struggle in both Pre-Algebra and Algebra. The cause is due to a lack of confidence in key middle school math concepts. Some students even struggle with multiplication facts taught in elementary school.
I invite you to continue reading to learn more about those important math concept
Where to Start in Middle School Math: Math to Know Before Pre-Algebra
When a seed sprouts and produces strong, supportive roots it provides a flourishing foundation for growth above it.
When building a house, a strong foundation must be built before other parts of the house can be added.
In the same way, we most successfully and confidently learn math by starting with the basics, as those basics support new learning.



1. Basic Math Operations in Middle School: Math to Know Before Pre-Algebra
Basic math operations are the foundation of math.
Providing students with instruction and practice with adding, subtracting, dividing and multiplying is the beginning of financial literacy for students, providing for them a basic skill to enable their independence in the adult world.
This means that we need to understand what it means to add, subtract, multiply or divide whole numbers before we are able to understand fractions, decimals, percent and numbers below zero.

2. Listing Factors in Middle School: Math to Know Before Pre-Algebra
As students learn multiplication facts, it is ideal for instruction to provide the meaning of the words, “factor” and “multiple”.
For example, in the following:
2 x 6 = 12
2 and 6 are factors.
12 is the multiple.
Beneath is a list of factors for 12 and 18.
When factors are multiplied, the result is a number referred to as a “multiple.”

3. Divisibility Rules in Middle School: Math to Know Before Pre-Algebra
After students have memorized multiplication facts, they commonly begin working division problems.
This is an excellent time to begin learning divisibility rules.
You may be familiar with some of these.
For example, a number that ends in zero is divisible by 10 evenly.
Take the numbers 30, 40, and 50.
All three of these numbers are divisible by ten as they each end in zero.
Using divisibility rules prepares students to list factors of large numbers and reduce fractions at a much faster rate, particularly if the numbers are large.
Each time students experience success in math, the more confident and prepared students will be to tackle the next level of challenge.
In the chart below you will find the basic divisibility rules.

Should you be looking for student practice pages with these divisibility rules and quick tips for finding number patterns for listing factors, I would encourage you to check out the following:

This is a 33 page product that provides students with instruction and practice for listing factors of numbers using divisibility rules and number patterns. It is also very helpful to use prior to factoring polynomials and simplifying radicals. Visit my store at: https://www.teacherspayteachers.com/Store/Bonnie-Stephan
4. The Greatest Common Factor in Middle School: Math to Know Before Pre-Algebra
Once students understand how to list factors by using divisibility rules and observing patterns of factors, students are prepared to understand the concept of finding the greatest common factor.
The greatest common factor, also referred to as the G.C.F., also plays a significant role in reducing fractions.
It is also useful in Algebra when listing factors to simplify radicals and factor polynomials.

5. Fractions in Middle School: Math to Know Before Pre-Algebra
Maybe now is a good time to take a couple deep breaths and sip a cup of chamomile tea.
Yes.
Fractions, decimals and percent serve as the # 1 challenge for students in both middle school and high school.
Merely mention the word “fraction” and you will see the class begin to cringe and groan.
On the other hand, it has been my observation that my students who are successful with fraction operations (adding, subtracting, multiplying and dividing) in middle school are confident and prepared to solve expressions and equations with fractions applied to Pre-Algebra and Algebra concepts.
Other related blog topics.
Proper Fractions, Improper Fractions and Mixed Numbers: What are They?
In the box below you will find a brief description of three types of fractions.
Students benefit from knowing the difference between these.
When adding, subtracting, multiplying or dividing, these same terms may be included.
For example, directions for completing fraction operations might include,
“Write the final answer as a mixed number, ” or “Change all mixed numbers to improper fractions.”

Converting Between Improper Fractions and Mixed Numbers: Math to Know Before Pre-Algebra
Once students are able to distinguish between proper fractions, improper fractions, and mixed numbers, they are ready learn how to convert from one type to another.

I often share with my students the importance of learning how to convert improper fractions to mixed numbers using the following example.
“So, after multiplying these numbers, we discovered through our calculation that Bob is going to need 23 / 4 gallons of paint.
Will the person at Bob’s local hardware store know what he is talking about if Bob gives the value 23/4, an improper fraction?”
I pause for a moment and wait for a response. After students arrive at the correct conclusion, I continue.
“You are right! Bob will need to provide a value in mixed number form. What will that value be?”
To extend the problem solving process, I might add that the hardware store only supplies paint in gallon-sized cans.
My next question: “How many cans of paint does Bob need to buy?”
“You are correct. Bob will have to buy six gallons of paint.”
The Least Common Multiple: Math to Know Before Pre-Algebra
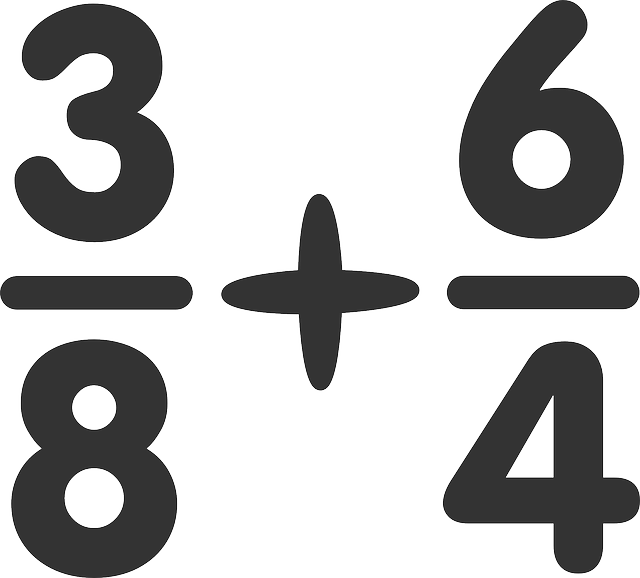
The least common multiple, also referred to as the L.C.M., is used when adding and subtracting fractions with unlike denominators.
Example: List the multiples of 8 and 4
8: 8, 16, 24, 32
4: 4, 8, 12, 16, 20, 24
The least common multiple is 8.
In many curriculums and textbooks the least common multiple and the greatest common factor are often introduced at the same time or at least within the same week.
Talk about confusion! Maybe you have been there.
I advise teaching the least common multiple concept a week or so prior to students being introduced to addition and subtraction of fractions with unlike denominators.
The introduction process includes:
1. Explaining what a multiple is
2. Explaining what common multiples are
3. Explaining how to identify what the least common multiple is
4. Practice listing multiples for 2 to 3 numbers to determine the common and least common multiple
By having this process down first, students are less overwhelmed when steps for adding and subtracting fractions with unlike denominators are taught as they already know how to find the L.C.M.
Below is a product the provides both instruction and practice for this skill.

This product provides both instruction and practice.
Visit my store at: https://www.teacherspayteachers.com/Store/Bonnie-Stephan
6. Decimals in Middle School: Math to Know Before Pre-Algebra
Place Value
Students need to learn the names of the values after the decimal point such as tenth, hundredth and thousandth.
This is important as it allows students to respond to directions such as,
“Round your final answer up to the nearest hundredth.”
When introduced to this concept, students often benefit from using a chart that illustrates these place values along with the terms used for each.
Compare and Order Decimals
This concept must be taught as decimal numbers can easily be mis-understood.
For example, when students are given two decimals such as 0.124 and 0.3 and are asked to determine which one is larger, students will often pick 0.124 as this number has more digits.
In this case, 0.3 is larger.
Understanding these concepts is also useful when comparing mathematical values and measurements in science.
Rounding Numbers
Rounding numbers is another skill that students commonly ask about. As mentioned earlier, students must first understand place value and the terms used for each.
Furthermore, questions in geometry related to finding perimeter, area, volume and surface area often ask for the final answer to be rounded to the nearest whole number, the nearest tenth or other place value.
Take for example, pi, a value used in finding the circumference and area of a circle.
Being able to round numbers such as pi = 3.14159265359… up to the nearest hundredth would indeed be most helpful as the number, pi goes on into infinity!
3.14159265359… rounded up to the nearest hundredth = 3.14 pi
7. Percent in Middle School: Math to Know Before Pre-Algebra
Students need to know what percent is and how to find the percent of a number.
Ratio and proportions may be taught before or in conjunction with percent as these topics are related to fractions and percent.
Students may next be be introduced to finding percent or determining the whole or part of a number such as:
“Seven is what percent of 52?”
“If there are 4 brown eggs and 10 white eggs, what percent of the eggs are brown?”
“Of the 7 cars, what percent are green?”
“What is 73 % of 52?”
Examples of Fraction, Decimal and Percent Applications from Middle School to High School


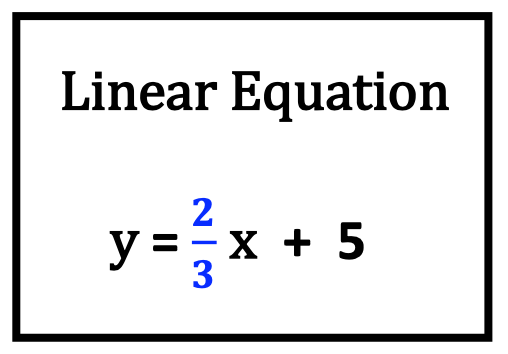


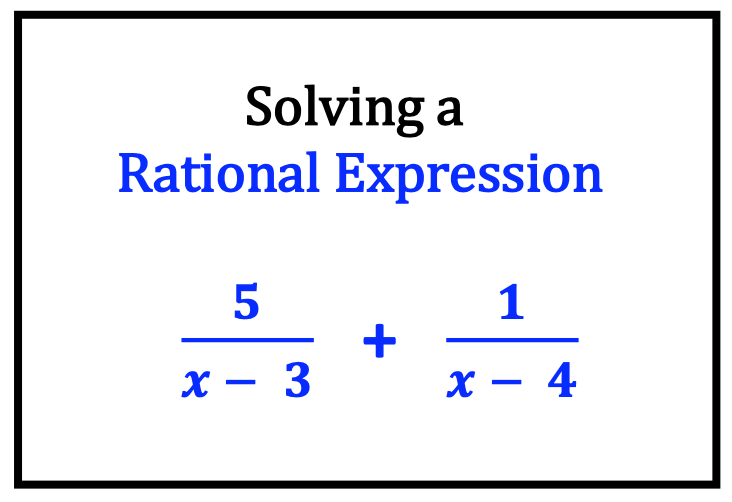
8. Math Applications with Life Skills
Being able to solve fractions, decimals, percent and the ability to round numbers is helpful in every day life!
See the examples below.
1. Calculating a tip at a restaurant
2. Determining whether a certain percent off an item is really a good deal
3. Understanding how interest works based on the amount of the interest rate for purchase or investing
4. Purchasing of an item in which total cost includes sales tax.
Consider an item with an initial cost is $ 100.00. If tax is 10 %, the total cost will be $ 110.00.
Consider a car that has a sticker price of $ 150,000, with a sales tax rate of 10 %.
The total owed in taxes would be $15,000.
5. Figuring the amount due for annual federal taxes
6. Constructing a project that includes precise measurement in millimeters



7. Let’s imagine you were comparing the cost between two beverage bottles of two different brands and considering the most economical purchase.
You look at both bottles. Both are different prices and both contain close to, but not the same amount in ounces.
To make matters even more interesting, you notice that the number of ounces listed for each bottle include decimal numbers.

8. You are wanting to make 5 batches of home-made chocolate chip cookies and you need to determine how to convert your measurements for each ingredient.
Understanding how to multiply fractions could come in pretty conveniently:
1 1/3 c. of sugar x 5, and you are on your way!
9. College Prep
A.C.T, S.A.T. or Other Similar College Entrance Exams
Low test scores are not necessarily due to not understanding trigonometry ratios.
Rather, it may be due to lack of a thorough understanding related to fractions, decimals and percent.
I recommend that any preparation for standard testing include evaluating student understanding of these three concepts, fractions, decimals and percent What you find may or may not surprise you. On the other hand, It will be a wonderful place to start as test questions for these exams include concepts related to these three fundamental math concepts. The easy exam questions could be as basic as adding two fractions with unlike denominators. Or, a question may also include a more complex question as such as finding the probability of an event.
Yes. It is the small stuff that makes a big difference!

In Conclusion …
Math concepts are best understood when concepts are presented in a logical and connected way.
May you have discovered the importance of building a solid math foundation one step at a time, providing students with knowledge they need to know before pre-algebra
May you feel empowered to ensure students understand each of these significant math concepts.




