Through the Eyes of a Student
Fraction problems on the page glare up at me. My pencil quivers!
Yesterday my teacher reviewed rules to use when solving fractions. Now those rules are floating around my head like different flavors of ice-cream, all melting together!
To flip or not to flip the fraction? Create like denominators? Then again, what were the steps for finding like denominators? L.C.M.? L.C.D.? G.C.F.??? Lowest terms? How do I know?
am SOOOOOOOOOO CONFUSED!!!
Now you may understand why I struggle with fractions.
- Content:
- Introduction
- 1. Three Forms of Fractions
- 2. Different Steps for Solving Fraction Problems
- 3. Use of Both the Vertical and Horizontal Method
- 4. Lack of Confidence with Basic Math Computations
- 5. Different Teachers Each School Year
- 6. Different Curriculums, Frequent Curriculum Changes
- 7. Fraction Operations Taught To Close Together: Adding, Subtracting, Multiplying and Dividing
- 8. Lack of Practice
- 9. The Internet
- Student Struggles with Fractions: The Big Picture
- Conclusion
1. Three Forms of Fractions

In elementary school, most students are introduced to proper fractions, improper fractions and mixed numbers. This is commonly accomplished through pictures, puzzles and other hands-on activities. Students provided with such experiences are able to more easily understand fraction operations. Despite these approaches, it is not unusual for some students to need a review of these basic concepts in middle school prior to the introduction of fraction operations. Such review will ease student struggle with fractions.
Furthermore, students must also be able to recognize the terms “proper,” “improper,” and “mixed numbers” as these terms are also included in directions such as,
“Write the final answer as a mixed number.”
Below you will see many possible arrangements of these three types of fractions:
Proper Fractions:
1 / 4 + 2 / 7
The top number is smaller than the bottom number.
Improper Fractions:
7 / 2 + 9 / 4
The top number is larger than the bottom number.
Mixed Numbers:
3 1 / 2 + 5 3 / 4
Mixed Number: Includes a whole number of 3 with a fraction of 1/2
Mixed Number: Includes a whole number of 5 with a fraction of 3/4
Proper and Improper Fraction:
3 / 7 + 9 / 5
Proper Fraction and Mixed Number:
4 / 5 + 2 1 / 3
Mixed Number: Includes a whole number of 2 with a fraction of 1/3
Improper Fraction with Mixed Number:
8 / 3 + 3 4 / 9
Mixed Number: Includes a whole number of 3 with a fraction of 4/9
2. Different Steps for Solving Fraction Problems

Likewise, not only are there three forms of fractions, there are also different steps for solving different types of fraction operations which also increases the student’s struggle with fractions.
Below you will discover the different operations and the steps for solving each one.
ADD and SUBTRACT FRACTIONS with LIKE DENOMINATORS:
Add or subtract the numbers in the numerator
Keep the numbers in the denominator
MULTIPLY FRACTIONS
Multiply the numbers in the numerator.
Multiply the numbers in the denominator.
DIVIDE FRACTIONS
Keep the first fraction as it is written.
Change the division sign to a multiplication sign.
Flip the last term.
ADD and SUBTRACT FRACTIONS with UN-LIKE DENOMINATORS
Find the Least Common Multiple for the numbers in the denominator.
Multiply by a number that will make both denominators the same number as the Least Common Multiple.
Be sure to multiply the numerator by the same number that was multiplied in the denominator.
REDUCE FRACTIONS
Reducing fractions is yet another process students will need to learn.
Reflection …
How many students have you taught that do not know the difference between the numerator and the denominator?
Have you ever recorded the number of times you find a need to re-explain what the Least Common Multiple is and how to find it?
And just when you think your students finally understand how to add, subtract, multiply and divide fractions, oh the times when you observe students searching for the Least Common Multiple when multiplying fractions, or other similar mis-calculations.
You are not alone. Hang in there!
3. Use of Both the Vertical and Horizontal Method
When reviewing middle school math curriculums and supplemental materials related to fraction operations it never ceases to amaze me as I observe all the different strategies used.
It is no wonder why students struggle with fractions!
Also interesting is the arrangement of each fraction problem. Below, notice the two different methods for arranging the same fraction operation.
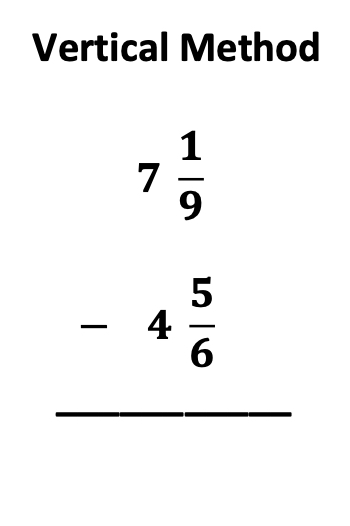
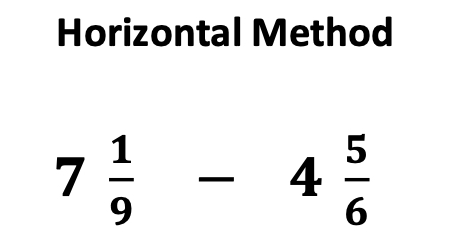
Furthermore, though the vertical method has been used most often in middle school, I am quite pleased to discover that more middle school math materials and curriculums are beginning to utilize the horizontal method.
The horizontal method appears to be utilized more often in high school, with the exception of simplifying complex fractions, a concept that may be taught in Algebra 2.
The Take-Away: With all the parts and pieces required to learn fractions, would it not be better for students to be introduced from the beginning to solve all fractions written horizontally?
Let’s consider all the ways horizontal forms of fractions occur in geometry and algebra. As you view each illustration, note how the horizontal method is applicable to common math formulas and equations.
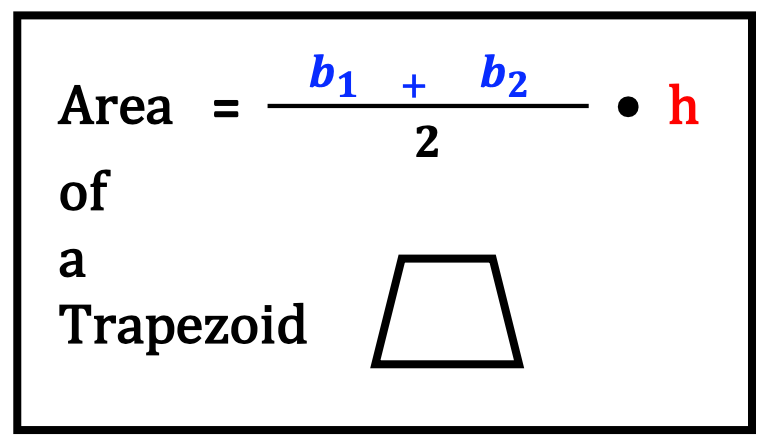
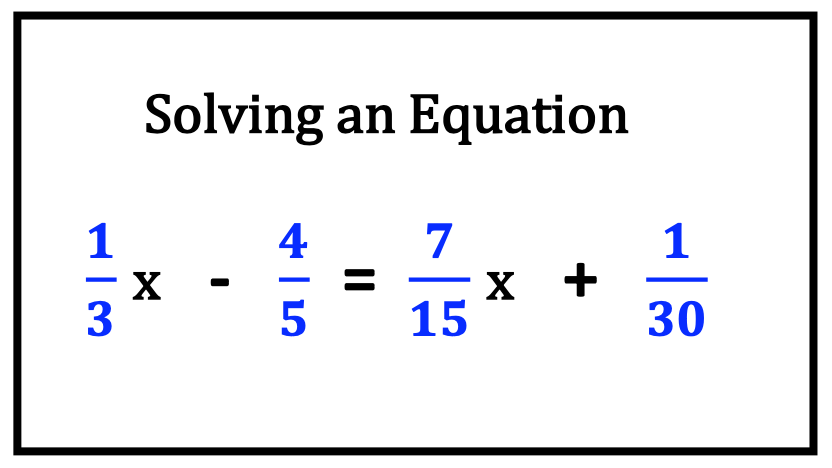
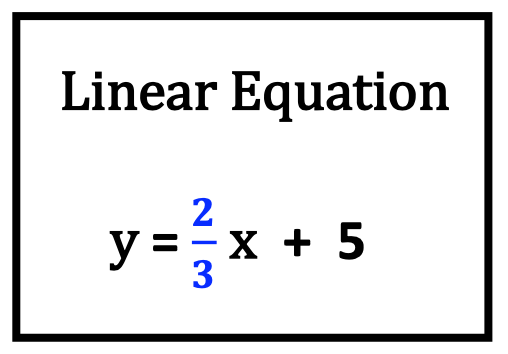
4. Lack of Confidence with Basic Math Computations
You are flipping through worksheet pages students have completed and notice multiplication and division facts are the cause for error in student answers.

Maybe you have given a timed test for multiplying fractions. As you reviewed test pages you discovered that some students had the correct answers, though they only completed half the test before it was over.
Prior to the fraction section being taught, you noted that these same students also struggled with processing basic multiplication facts in other prior math related topics.
When students do not know how to process basic math facts such as multiplication or struggle to remember the steps for dividing fractions, over time students can become frustrated and discouraged with math in general. The mere student frustration over a lack of basic math facts continues to echo why
students struggle with fractions!
5. Different Teachers Each School Year
Depending how middle school math classes are set up, students may have a different math teacher for each grade, meaning that each teacher may have a different way of teaching fractions than the teacher from the year before.
Or, students who move often will have a different teacher who may also approach fractions in a different way.
6. Different Curriculums, Frequent Curriculum Changes
Let’s imagine you are traveling through a new town, before GPS. You come across a detour. There are signs that point out the different route to take. As you drive through this unfamiliar town, there are many distractions; flashing lights, stores with big signs, and it is raining. If that isn’t enough, the person driving behind you appears to be in a hurry. In the chaos of sensory overload, you think you may have missed a sign. Yes, you now recognize that you are lost.
Lost. This is how students feel when fractions are taught differently from year to year. How many times have your students said,
“This isn’t the way we learned it last year.”
7. Fraction Operations Taught Too Close Together: Adding, Subtracting, Multiplying and Dividing

Trying to cover every math topic in middle school can be quite daunting. Due to this, fraction operations are covered quickly, one after the other in order to “get it done” before moving on to the next section.
Also, when coming to the end of a fraction section, it is not unusual for students to get mixed up between the different ways to solve each kind of fraction problem. Yet, we hope that students remember as much as possible the following year.
Unfortunately, in the following year these topics are taught once again at an even faster pace as there is even more to cover, including pre-algebra concepts such as integers, which is also a topic of challenge for some students. So yes, a whirlwind of information that does not settle in is a full blown recipe explaining why students struggle with fractions!
So what’s a teacher to do?
Solutions:
1. “A Fabulous Friday” : use that day for students to go through stations, some of which include fraction operation review in the form of quick check: quizzes, games, puzzles, or task cards.
2. Bell Work: Provide students a fraction operation to complete for every day of the week. Be sure that each day there is a different fraction operation. For example, Monday: addition and subtraction with like denominators, Tuesday: multiplication, Wednesday: division, Thursday: adding and subtracting fractions with un-like denominators. Friday: all operations
3. Posters: If students forget how to solve a certain type of fraction problem, place posters in the room which illustrate the steps for solving each type of fraction operation. Have students not only answer the problem, but also illustrate the steps for solving as illustrated on the poster.
4. Word Problems / Application Problems: For students who appear to have mastered fraction operations, provide word problems for challenge.
5. Students Challenge Students:
Day 1: Student teams are formed. Each team writes and solves five fraction problems.
Day 2: The next day, students forward the five fraction problems from one team to the next.
Each team that is able to solve another team’s questions correctly, earns a point.
This process could be repeated daily or once a week.
8. Lack of Practice
You watch an instructional video that has so much information you need to watch it over and over again as you did not understand it the first time.
Students commonly experience this information overload with fractions. Due to complexity of fraction operations, these skills must be reviewed even after completing the math section on fractions.
For example, while covering decimal and percent, I continue to review fraction operations. To keep decimals and percent in check, I give my students a fraction problem, ask them to turn it into a decimal and then a percent as I want my students to be able to make connections between fractions, decimals and percent all year long.
Likewise, as students practice converting fractions to decimals, students are also asked to round decimal answers to the nearest hundredth’s place. This practice prepares students for future math problems related to money calculations involving conversion between decimals and percent.
Looking for ways to to decrease student struggle with fractions!? My students continue fraction, decimal and percent practice till the end of the school year. This has made a big difference which significantly helps in carryover from year to year.
9. The Internet

I love doing searches on the internet!
Need a new recipe idea for the holidays? Just enter what you are looking for. Within seconds, several links pop up on the screen. Click on a couple ideas and before you know it, you have been sent to so many interesting sites that now you find yourself watching a video about cruises to the Caribbean!
The Flip-side of Internet Searches: For those who are looking for the perfect way to teach fractions, the search begins with much hope. Next, before you know it, two hours have gone by and you have seen so many methods that by now you are more confused than when you started due to the the many methods discovered.

Furthermore, our students are most internet savvy. To make matters more interesting, the internet is not only a general information provider that helps students do research at a much faster pace, it now provides access to special tools that calculate fractions and other math calculations, some even showing the steps for each problem.
While it is great that our students may find ways to solve fractions and other math problems using the internet, my biggest concern is whether they truly understand what they are copying down.
This is where pop quizzes come in handy. After students begin to work the problems, I walk around and observe student performance which often provides me with great feedback to determine if homework performance corresponds with in-class performance. From that point, I am much more aware of student understanding.
Student Struggles with Fractions: The Big Picture
It has been my observation that math anxiety begins in middle school. The culprit is most commonly fraction operations.
In addition, math anxiety and poor understanding of fractions, decimals and percent problems also contribute to challenges in algebra and geometry. This being the case, it is not surprising that these challenges are also reflected in math scores on the A.C.T. and other similar tests.
Furthermore, as students begin their college experience the A.C.T. math score, or other math test scores are commonly used to determine what math courses a student is prepared to take. Students who do not meet the required math test score may be required to take remedial math courses prior to taking a college level math course. Remedial courses required may range in levels from middle school to high school algebra concepts, depending on student testing scores.
Consequently, while working with students taking remedial classes I discovered that fractions were most often the topic of greatest challenge for students.
Conclusion
As a teacher or parent, you may be able to share your own stories regarding the struggles students experience with fractions; a concept many students struggle with from year to year. Take heart, as our awareness of these struggles is the beginning to student math success! Be proactive in the now, wherever that may be.
In closing, I leave these words of encouragement:

By identifying
the challenges
at any level,
we can rise up
and
meet any challenge.