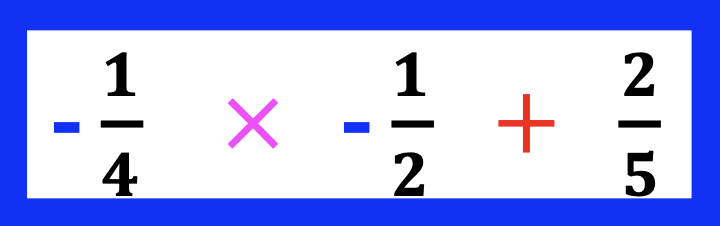Are math problems with a combination of fractions and integers confusing for your students? Discover how to ease this anxiety through preparation.
#1 – Review Fraction Operations
Do your students experience math challenges when given problems that combine fractions and integers? I’ve been there and have found solutions to meet these challenges
The solution? Anticipate and intervene before moving forward to integers.
Furthermore, due to student “fraction trauma” in middle school, our students enter the classroom with fraction anxiety. On the first day of class, I begin with a fraction review. On the second day, I add a new fraction operation. Homework includes fraction operations from both days.
In addition, I continue this review in homework assignments throughout the year. Review could be in the form of morning work, bell ringers, math test homework reviews, and even nested in a test.
Why do this review?
It will save you tons of time and frustration as you introduce integer rules as applied to fraction operations with and without parenthesis. It saves you time having to review fraction operations at the same time you are trying to reach those students who are struggling with integer concepts.
On the other hand, are you looking for high-school-appropriate resources that provide fraction practice? The following resource includes an example page and 25 practice pages. Each page includes all fraction operations. Answers are included.
Click on the link below the image: Fractions, Decimals, and Percents: Practice for High School Review.

#2 – Integer Rules
After students are confident with fraction operations, they will be ready to learn the rules for using integers.
In addition, as students learn integer rules, include practice with problems that include parentheses. For some students, parentheses appear as visual distractions or what I like to refer to as “visual clutter,” meaning that it is one more symbol for students to visually navigate. The more details in a math expression, the more students must mentally and visually sort.
Furthermore, the use of color-coding or high-lighting may also be useful to help students distinguish between the parts. This is illustrated in the example below. Notice how the operation sign for multiplication is in pink, whereas the negative numbers are in black.
For example, let’s imagine the problem, -4 x – 2 = is on a homework page. It would not be unusual for students to inquire whether this was a subtraction or multiplication problem. The highlighted multiplication sign is enough to help the student recognize the operation.
On the other hand, it is important to use the color-coding process sparingly, as too many colors may also contribute to “visual clutter”.


After students understand basic integer rules with numbers without fractions, they will be ready to apply integer rules with fraction operations.
Are you looking for resources to introduce integer concepts?
Integers, Strategies, Posters, and Practice is a resource you may find helpful. It includes 68 practice problems, an answer key, and 10 posters. Includes both vertical and horizontal number lines. Vertical format prepares students to solve equations with signed numbers. Click on the link below the image to learn more. Click on the link below the image.
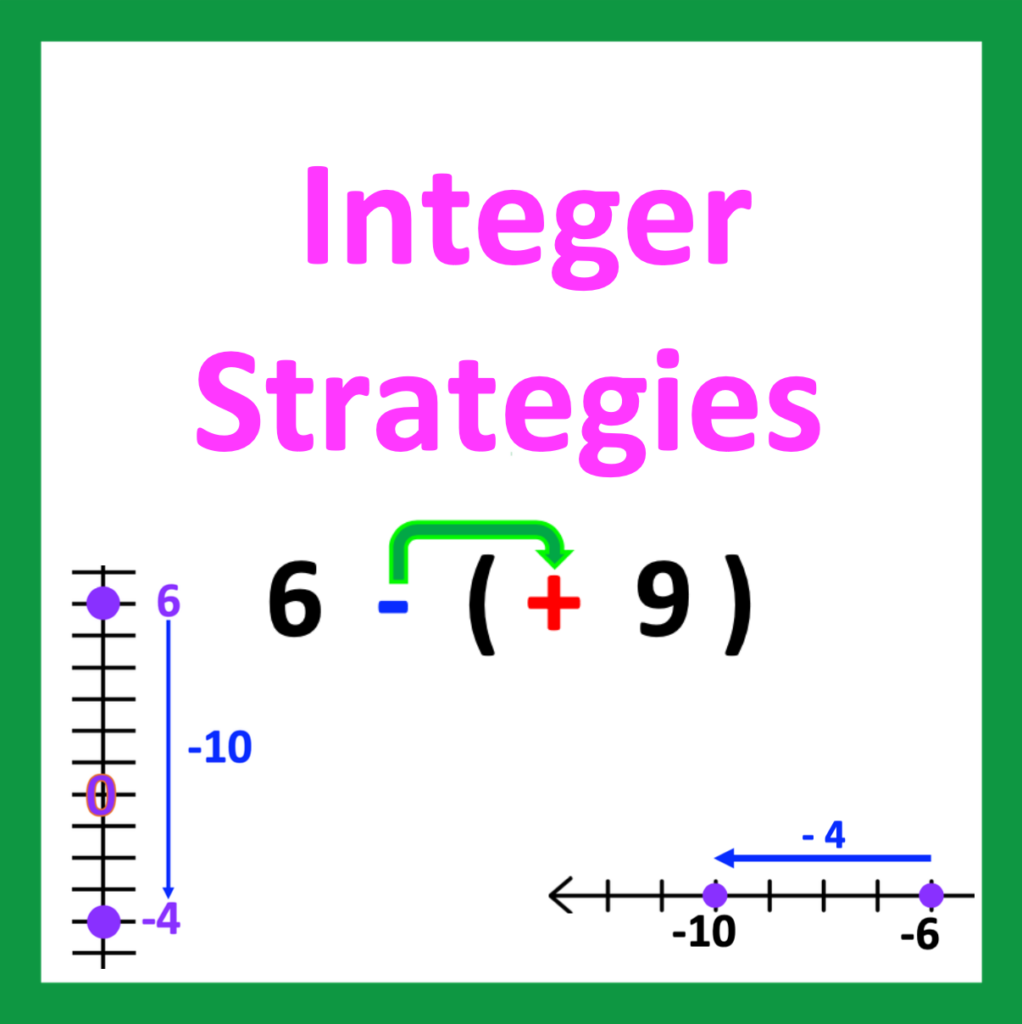
https://www.teacherspayteachers.com/Product/Integer-Strategies-Posters-and-Practice-11444768
#3 – Combine Fraction and Integer Problems
Are students able to perform all fraction operations? Do they know how to solve integer problems with and without parenthesis? If yes, you are ready to teach students how to solve combined fraction/integer problems!
As you begin this journey, introduce these concepts in the following order:
A. Simplifying Fractions
B. Adding and Subtracting Fractions with Like Denominators
C. Multiplying Fractions
D. Dividing Fractions
E. Adding and Subtracting Fractions with Un-Like Denominators
F. Fraction Operations with More than Two Terms
Any time we slowly build on what students know, students will feel less overwhelmed with new information.
A. Simplifying Fractions
If you have students who are overwhelmed thinking through many steps at the same time, divide the verbal instructions into two parts. This is also helpful for students with mental math calculation challenges. For example, when simplifying fractions I will share concepts in two separate steps.
“Signs, first.”
(Pause).
“Then, numbers.”

B. Adding and Subtracting Fractions with Like Denominators
Next, introduce fractions with like denominators. Before doing an example with a parenthesis, share a simple problem with the same signs, though no parenthesis, 4 – (-3) =
This mentally prepares students for the integer signs.
Next, give a simple fraction example: 4/5 – 1/5 =, and ask students to recall steps to solve the problem. After this, students will merge the two concepts with greater confidence. This strategy may be used with other problems.
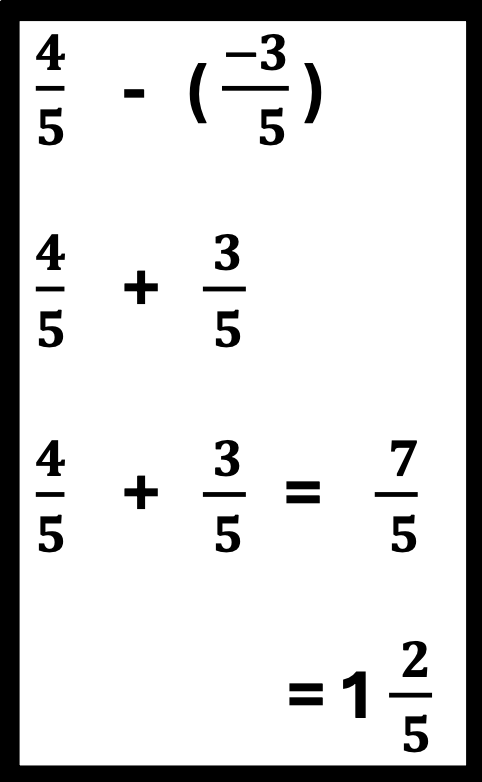
Also, though the answer 7/5 is correct, I recommend that my students turn the improper fraction into a mixed number. This practice is useful for word problems.
C. Multiplying Fractions and Integers
When multiplication of fractions is taught, the use of color-coding is helpful in identifying the operation.
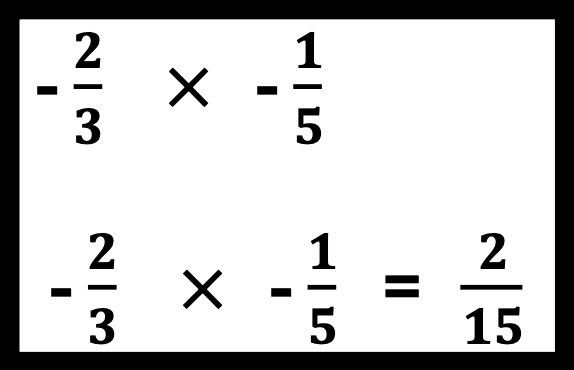
D. Dividing Fractions and Integers
When dividing fractions, it is ideal to color-code the operation in the problem.
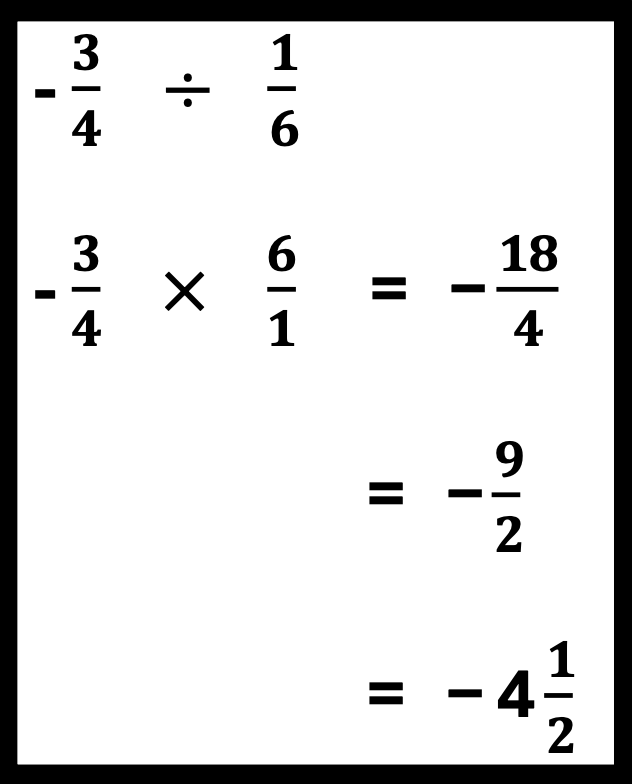
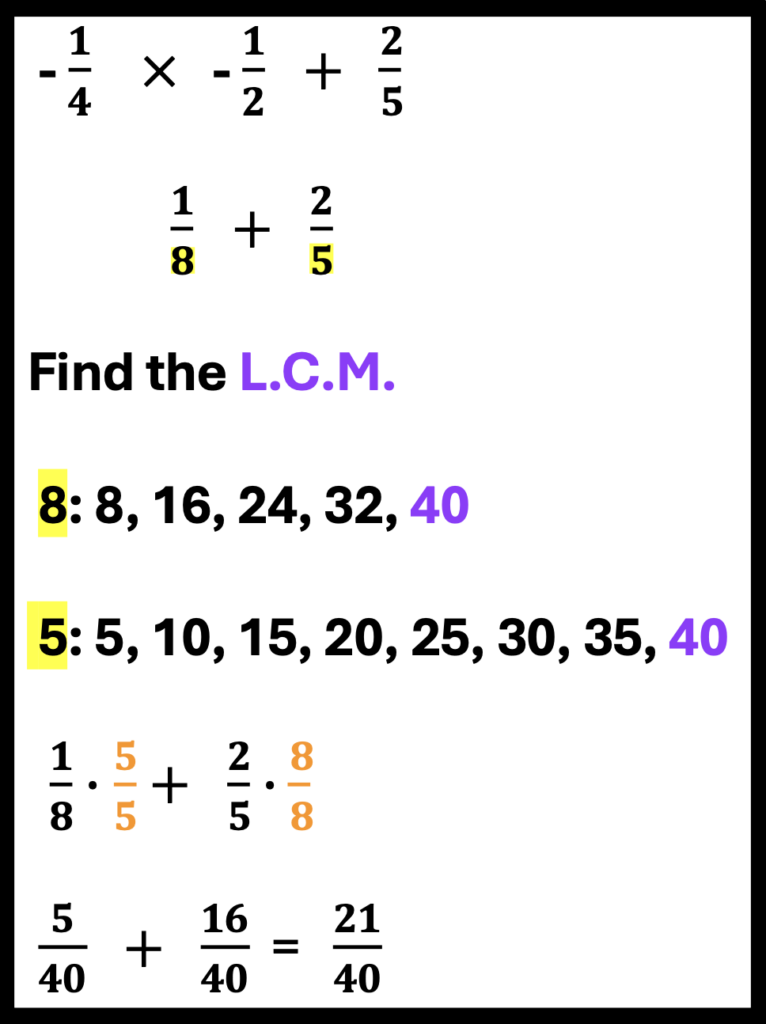
E. Adding and Subtracting Fractions with Unlike Denominators
Adding and subtracting fractions with unlike denominators adds more layers of steps; finding the least common multiple, (L.C.M.) to create like denominators. If students have continuously practiced all fraction operations up to this point, they will understand these problems.

F. Fraction Operations with More than Two Terms
Problems with more than two operations baffle some students. The most often asked question is where to begin.
On the other hand, if students have been introduced to the order of operations, they may know that multiplication comes before division.
If the order of operations has not been introduced, it can be introduced, now.
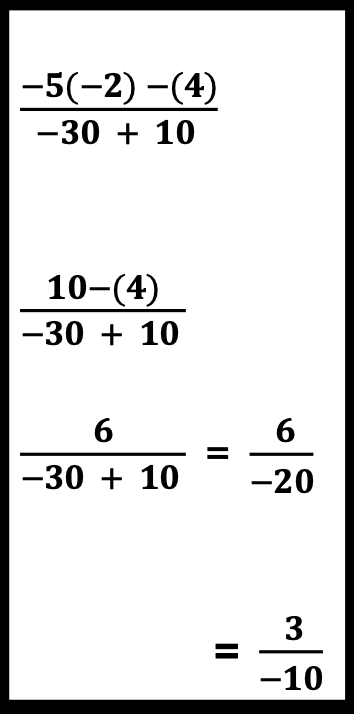
#4 – Mixed Review of Fractions and Integers
Furthermore, just as a review of fraction operations is important before introducing fractions, daily practice of problems that include a combination of fraction operations and integers is also significant.
Conclusion
When students are confident with fraction operations and integers, they will be successful with problems that combine fraction operations and integers.
Other Related Posts
- How to Successfully Teach Fraction Operations
Research: How Important are Fractions, Decimals and Percents
9 Reasons Why Students Struggle with Fractions
Introducing Integers: Best Methods with Negative and Positive Numbers
How to Teach Integers for Success for Order of Operations, Part 1
How to Teach Integers for Success for Order of Operations, Part 2
How to Teach Integers for Success for Order of Operations, Part 3
Looking for More Materials?
Click the button below to view more of my educational resources!