You are teaching students how to convert between fraction, decimal, and percent only to discover question marks etched in the faces of your students. After responding to a few questions, it appears as if most of the questions are related to math concepts students have already been taught a year or so ago. What are those other math concepts? Keep reading and you will discover how to successfully prepare students to perform conversions between fractions, decimals, and percent.
Contents:
- Introduction
- 1. Visuals Representing Fractions, Decimals and Percent
- 2. Division
- 3. Place Value and Rounding Numbers
- 4. Reducing Fractions
- Conclusion
Just as fraction operations are a challenge for students, the conversion between fractions, decimals and percent is another common challenge. To prepare for these concepts it is helpful to consider the other math skills sandwiched between the steps for doing these conversions. This can be provided with visuals and review of division, place value, rounding numbers and reducing fractions.
1. Visuals Representing Fractions, Decimals and Percent
Providing visuals is key for understanding fractions, decimals, and percent. When students can see what we are talking about, they process new concepts with greater understanding. On the other hand, if they do not know what we are talking about and cannot visualize a concept they will struggle to make connections between what we are saying and what we want them to do.
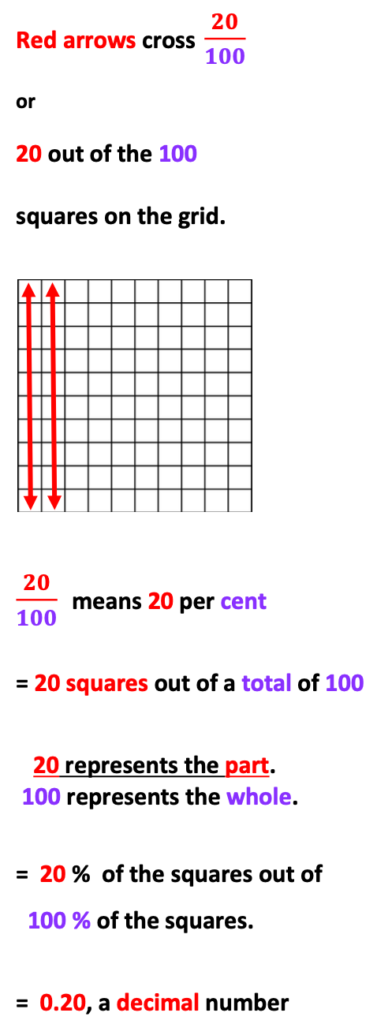
A great visual tool for both student and teacher includes the use of a dry-erase 10 x 10 grid representing a value of 100. Grids may also be placed in page protectors and drawn on with dry-erase markers.
If pre-made grids are not available, graph paper and highlighter pens also work.
10 x 10 grids help students recognize the representation of 100. Next, students will recognize that each single square = a value of 1.
Also, if each square represents a value of 1, we can also say that 1 represents 1 percent. Likewise, if there are 100 squares, we can also say that 100 represents 100 %.
In regards to fractions, if 40 squares out of 100 are colored in, it is visually easy to recognize that we could also say that 40 % of the squares are colored in.
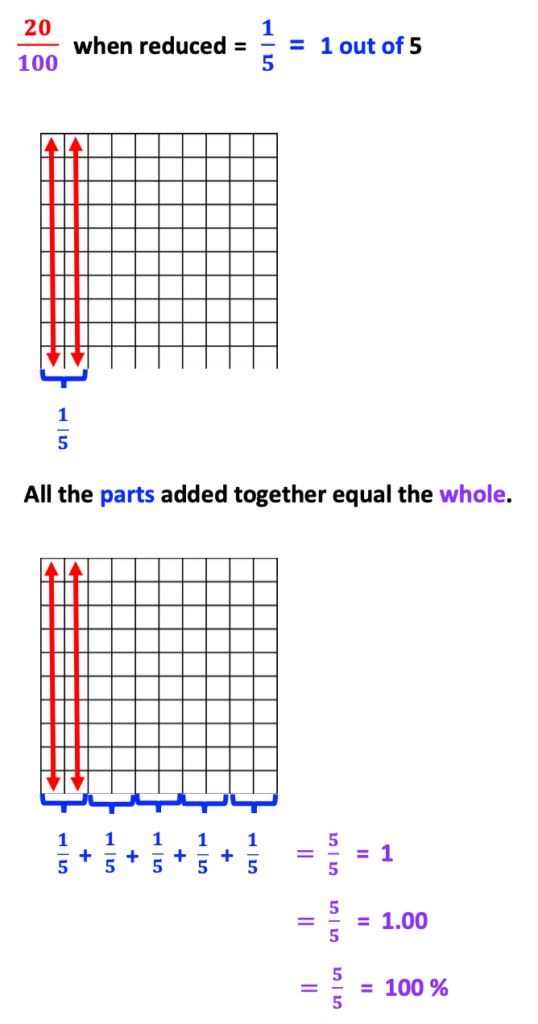
Also, if we know that the 10 x 10 grid represents a whole value of 100 and 40 of the squares are colored in, we can determine that 60 squares remain without color: 100 – 40 = 60. With this in mind, if we convert 100 to 1 whole we can also say: 1.00 – 0.04 = 0.60, as decimal numbers.
Below are more examples.
2. Division
Aside from providing visuals representing conversions between fractions decimals and percent, a review of division is also helpful as it is used when converting a fraction into a decimal. Some students may have accommodations that allow use of a calculator.
Below is an example illustrating steps for converting a fraction to a decimal, requiring the operation of division.
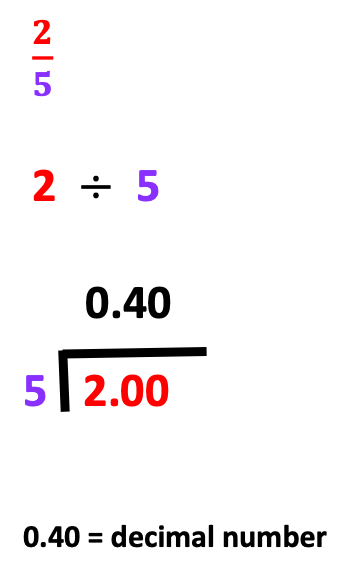
3. Place Value and Rounding Numbers
A common hiccup for students converting between fractions decimals and percent is a lack of place value awareness. In particular, place values to the right of the decimal tends to be challenging for some students as the order of each value appears backward to the order of the values used for whole numbers. Students must also remember to name values to the right of the decimal ending with “th”.

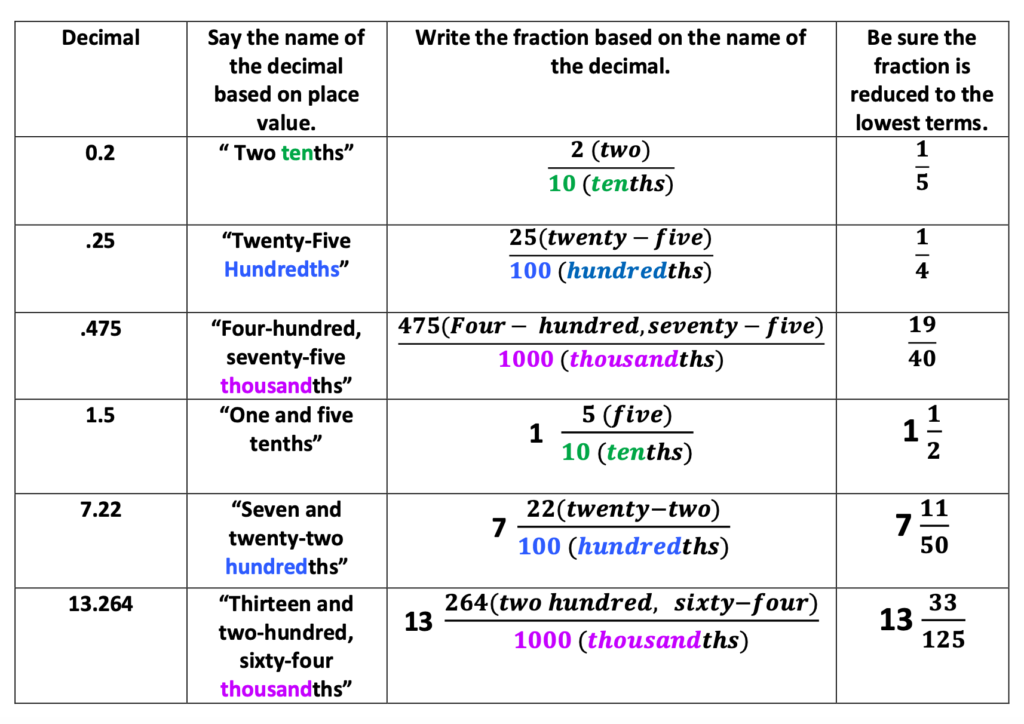
To better understand numbers to the right of the decimal, students will benefit by writing these numbers in words.
Using a place value chart, practice writing words that express decimal numbers. This helps students more clearly recognize the names of various place values. It also prepares students to convert percent and decimal numbers to fractions. See the example below.
Furthermore, place value and rounding are important when fractions are converted to decimals. For example, a decimal answer may result in repeated numbers to the right of the decimal point such as 1/3 = 0.3333333 ….
A decimal answer could also result in a list of multiple numbers to the right of the decimal point such as 22/7, pi = 3.141592653…. Such a result will require the number to be rounded to obtain the final answer. Below is a fraction that when converted to a decimal, results in repeating numbers.


These are the first three strategies that increase student success for conversions between fractions decimals and percent.
4. Reducing Fractions
Once students understand place value and rounding, a review of reducing fractions is useful when converting percent and a decimal to a fraction. There are two methods I recommend for this.
Method # 1: The GCF Method

This method is useful when reducing fractions with numbers less than 100.
For more details for reducing fractions, click on the link below:
How to Successfully Prepare Students to Reduce Fractions
https://ledtodiscover.com/middle/how-to-successfully-prepare-students-to-reduce-fractions-2
Method #2: Divide by 100, 50, 25,10, 5, 4, 2 or a number that appears related to the fraction using number sense.
This method is useful with fractions which include a denominator of 1000. I also encourage students to use number sense to consider the greatest common factor.
For example, 1000 divided by 2 = 500. When 500 is divided by 2, the result is 250. With practice, students begin to notice that these numbers show up quite often when reducing fractions with 1000 in the denominator. On the other hand, other fractions may need to be further divided to reach the lowest terms.
Also, while viewing the example below, notice that 5 is the obvious greatest common factor. After dividing the numerator and denominator by 5 the fraction is fully reduced.

Conclusion
A review of previously learned math concepts included in steps for converting between fractions, decimals, and percent provides a smooth pathway that best allows students to absorb new information. Practice of these concepts helps to solidify student understanding and confidence for the concepts reviewed and for those to come.
You’ve got this!