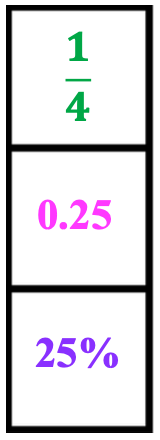
Fractions! Decimals! Percent! Now to convert between the three. It may sound like a significant challenge. And yes, there are so many different methods. You can do this! Keep reading to learn helpful strategies that will help you easily introduce how to convert between fractions, decimals, and percent.
Contents:
- Introduction
- 1. Visuals
- 2. Horizontal and Vertical Organization
- 3. Student Observation and Discovery Approach
- The Why
The How - Variations of this Activity
- Fraction to Decimal
- Decimal to Percent
- Percent to Decimal
- Decimal to Fraction
- Percent to Fraction
- The Why
- Conclusion
Prior to reading this blog, you may be interested in the blog, “Fractions, Decimals, and Percent: How to Successfully Prepare Students to Perform Conversions.”
If you have already read the above blog you will find visuals for fractions, decimals, and percent mentioned in the blog that follows as well. Visuals are significant as they help students see the math which helps the math make sense.
1. Visuals
Providing visuals is key for understanding fractions, decimals, and percent. When students can see what we are talking about, they process new concepts with greater understanding. On the other hand, if they do not know what we are talking about and cannot visualize such a concept, they will struggle to make connections between what we are saying and what we want them to do.
A great visual tool for both student and teacher includes the use of a dry-erase 10 x 10 grid representing a value of 100. Grids may also be placed in page protectors and drawn on with dry-erase markers.
If pre-made grids are not available, graph paper and highlighter pens also work.
10 x 10 grids help students recognize the representation of 100. Next, students will recognize that each single square = a value of 1.
Furthermore, if each square represents a value of 1, we can also say that 1 represents 1 percent. Likewise, if there are 100 squares, we can also say that 100 represents 100 %.
In regards to fractions, if 40 squares out of 100 are colored in, it is visually easy to recognize that we could also say that 40 % of the squares are colored in.
Also, if we know that the 10 x 10 grid represents a value of 100, and 40 of the squares are colored in, we can determine that 60 squares remain without color: 100 – 40 = 60. With this in mind, if we convert 100 to 1 whole we can also say: 1.00 – 0.04 = 0.60, as decimal numbers.
Below are visual examples, beginning with a fraction
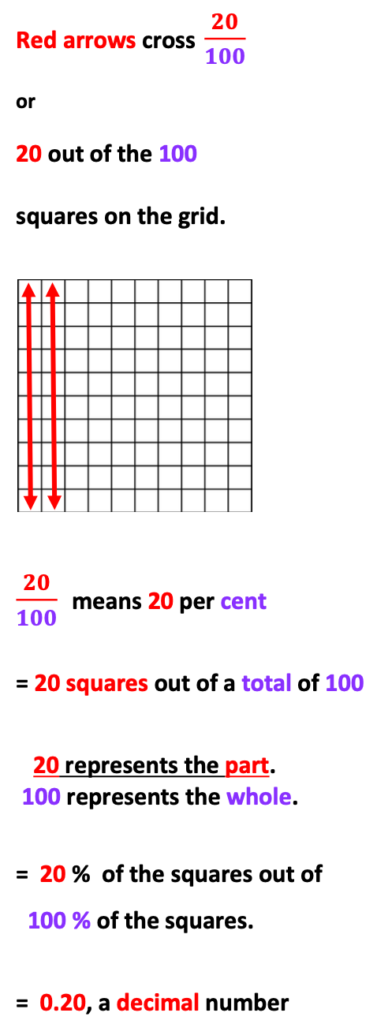
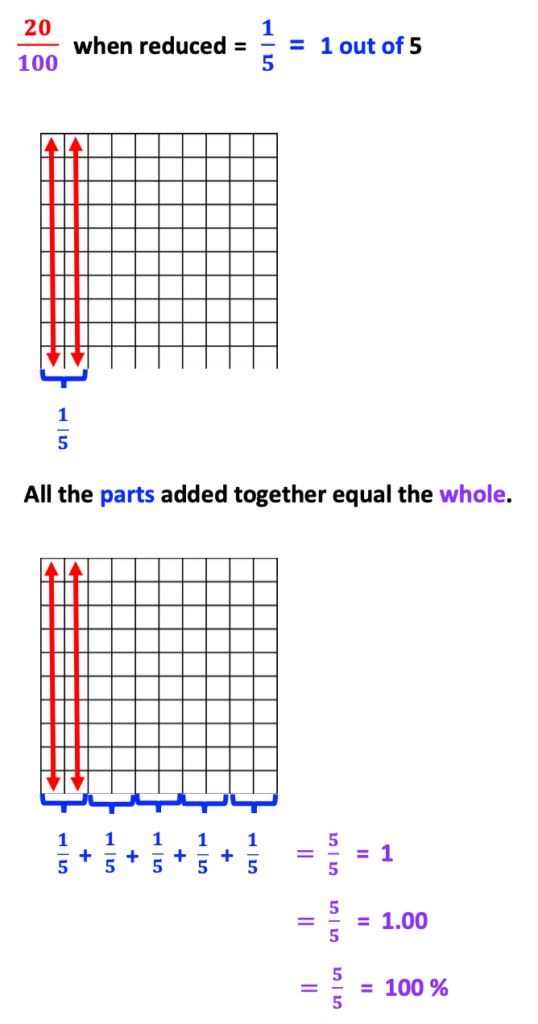
Notice how much easier it is to understand this concept with the 10 x 10 grid.
2. Horizontal and Vertical Organization
Furthermore, by arranging examples in a logical visual arrangement, students are better able to follow and align their written work.
For example, as you view the conversions to and from a decimal and percent, the numbers are lined up vertically. Graph paper is also useful for helping students keep numbers with decimals in line.

On the other hand, when converting from decimal to a fraction, or percent to a fraction, the arrangement begins in vertical format, though changes to a horizontal format when converting to fraction form. Viewing fractions from left to right helps students think about both the numerator and denominator alignment.
3. Student Observation and Discovery Approach
The Why
How often do we give students a list of steps to complete for converting between fractions, decimals and percent only to find that they still need to be reminded of the steps?
Instead, encourage students to observe the problem fully worked out, though without written instructions
The How
First, illustrate the problem-solving process for students from start to finish without using words. Such a problem could be written on the board or shared on the classroom screen.
Second, ask students to write their own set of directions based on their observations. Emphasize that each step must be numbered and include as many details as possible.
This activity requires more creative brain energy which helps students to think longer about the process. When students contemplate the process for an extended time, they are more likely to remember the steps.
This project can be completed individually, in small groups of 2 -3, or as a whole class. :
Variations of this Activity
# 1: After students have written directions, students may compare their observations with each other. At that time, they may discover other steps that they did not think of and may include these with the list they have started.
# 2: Students who are confident and accurate with conversions may “teach” peers how to write the directions or complete the problem.
# 3: After students have written their directions, the teacher collects all papers to determine student understanding.
*When pairing or grouping, be sure to create groups in which there is a student with good writing and language skills paired with a student who may need more assistance with these skills.
When students work in a small groups, each student should have a specific role to play.
All should participate by describing observations.
Choose someone to:
1. provide the final verbal direction
2. write out the verbal direction
3. solve the calculation
(Depending on the class or group of students, check to see if students have accommodations
allowing them to use a calculator).
Following are charts with examples listing both the problem and possible correct responses students may provide. Three of the charts also include “Teacher Notes” where I include other suggestions. You will find these notes on the chart in light blue print.
Fraction to Decimal

Decimal to Percent

Percent to Decimal

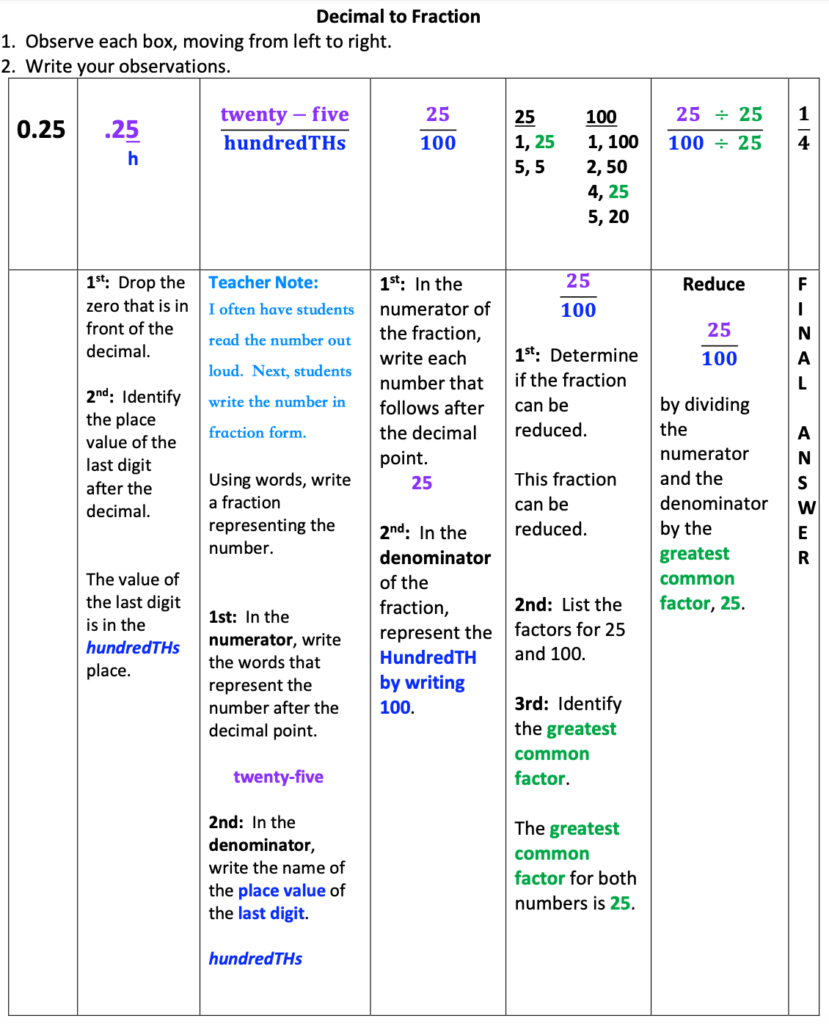
Decimal to Fraction
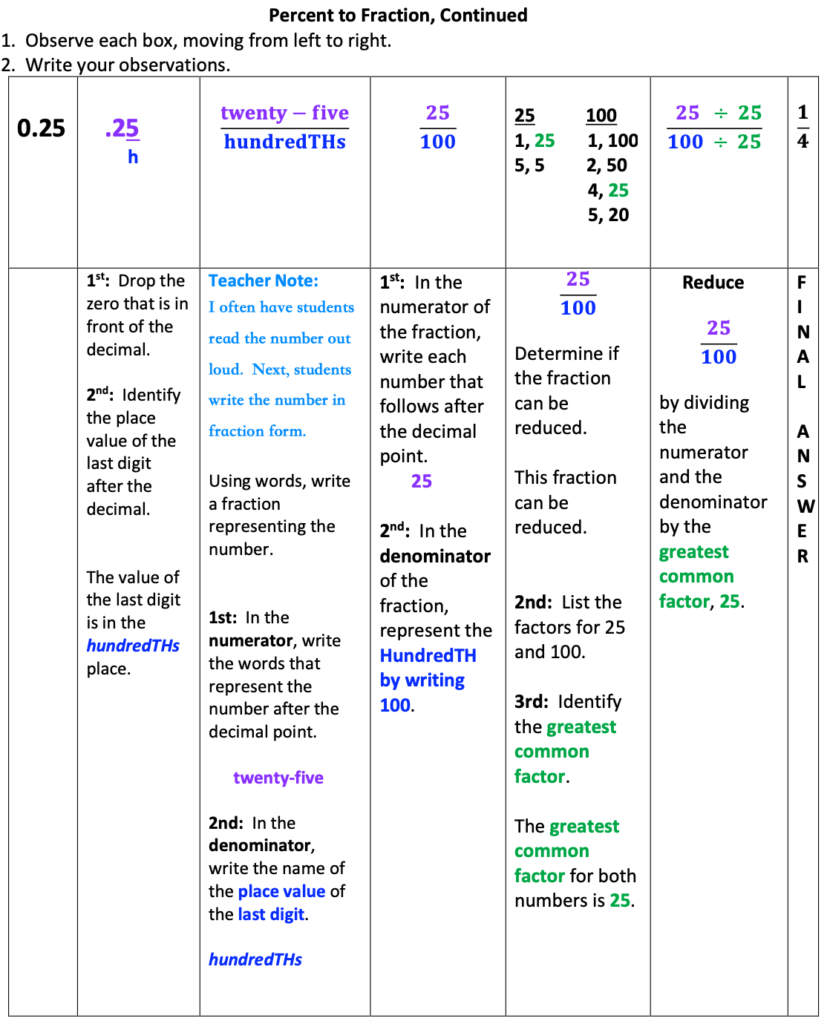
Percent to Fraction

Conclusion:
Using visuals, organizing problems in logical alignment, and use of student observation and discovery are effective ways to approach conversions of fractions, decimals, and percent. Following the observation and discovery approach, it is advisable to provide students with instruction for concepts missed.
Ok, so maybe you are wondering where to begin with these ideas. I have already created a print-and-go product that you may use that provides the format for student practice that you observed in this blog. To be provided with print-and-go materials for the student activity, visit my store where you will find: Convert Between Fractions, Decimals and Percent by Discovery!