Are you ready to introduce the Cartesian Plane? Are you looking for a way to pave a smooth foundation for other topics such as graphing points and writing equations? Keep reading and you will discover strategies for how to successfully Introduce the Cartesian Plane.
- Introduction
Thoughts on Teaching the Cartesian Plane: Do You See What I See?
Directionality and Figure Ground
“What Does This Have to Do With the Cartesian Plane?”
Where to From Here?
The Quadrants of the Cartesian Plane
The X and Y-Axis, and the Origin
X: East and West, Y: North and South
Numbers on the X -Axis
Numbers on the Y-Axis
The Big Picture the Cartesian Plane
Thoughts on Introducing the Cartesian Plane: Do You See What I See?
Maybe you have students who demonstrate the following challenges.
When using directional terms such as “right” and “left,” students glance back at you, pause, and bless their hearts, go the opposite way.
On the other hand, have you ever made a more complex statement such as,
“Write your name in the lower right corner of the page,” only to discover students wrote somewhere else?
Now that is a tough one for even the average student.
On the other hand, maybe there is a student with a box of markers, pencils, and erasers. As you watch, it takes the student for what seems like forever to find a particular marker. Maybe you glance over the student’s shoulder and see it right away.
Furthermore, we cannot forget the dear student that struggles to find where we are on a worksheet? If I asked the student why this occurred, the answer would not surprise me. The following is what I might hear:
“I know it is here on the page somewhere, but after I looked up at the board and then back at my paper, it disappeared!”
Recognizing and compensating for my own directional and visual-perceptual challenges, I truly believe the student’ response.
Directionality and Figure Ground
When using the word, “directionality” I am referring to our awareness of right, left, up, down, in, out. In language, we refer to these words as prepositions. You may have also heard individuals state that they are “directionally” challenged,” when describing challenges in completing various tasks.
Figure-ground is a visual skill that allows us to find what we are looking for in the middle of a mixture of other items. Imagine you are looking for an object in your desk drawer that you throw everything in that you don’t know what to do with. When you are looking for that particular item in that same drawer, add to it that you are stressed and in a hurry to find it, you will likely be able to relate to the student who can’t find a marker or loses the place on a page.
“What Does This Have to Do With the Cartesian Plane?”
Everything.
When we introduce students to the Cartesian Plane, directional terms are constantly being used. Here is a list of some of them:
Counter-Clockwise
Horizontal
Vertical
Horizontal Line
Vertical Line
Center
Left
To the left
To the right
Up
Down
Negative numbers to the left
Negative numbers going down
Positive numbers going to the right
Positive numbers going to the left
Positive infinity
Negative infinity
Figure-Ground challenges occur when the material is written with small print and images are very close together. Some students, when giving their best effort to find parts of the whole may share that even with their best efforts, the information on the page begins to move around as if swimming around on the page. In a worse-case scenero, some students even experience nausea in attempts to find and decipher such images.
Likewise, visual challenges with part and whole also come into play when viewing the Cartesian Plane. For example, when some students struggle to differentiate where x begins and y ends if the graph is drawn in one color. The use of different colors for the x and y axis helps students quickly identify that they are two parts of the whole. Otherwise, it looks like one whole image.
Where to From Here?
Now that we recognize some of the challenges students encounter with graphing concepts, we can now consider strategies to help our students understand the concepts.
When introducing concepts, I try to think of concepts that students can relate to, or even visualize. If they can see it, they are more likely to believe it. If they believe it, they will more likely remember it.
This is the case with quadrants. One of the more challenging concepts to remember where to begin and what direction to go in. In the following example, I use a clock.

Though I could have placed an arrow going from the first quadrant, and then to the second, third, and 4th quadrants, I would much rather that the students draw their own arrow. This helps them to see and feel what counter-clockwise means.
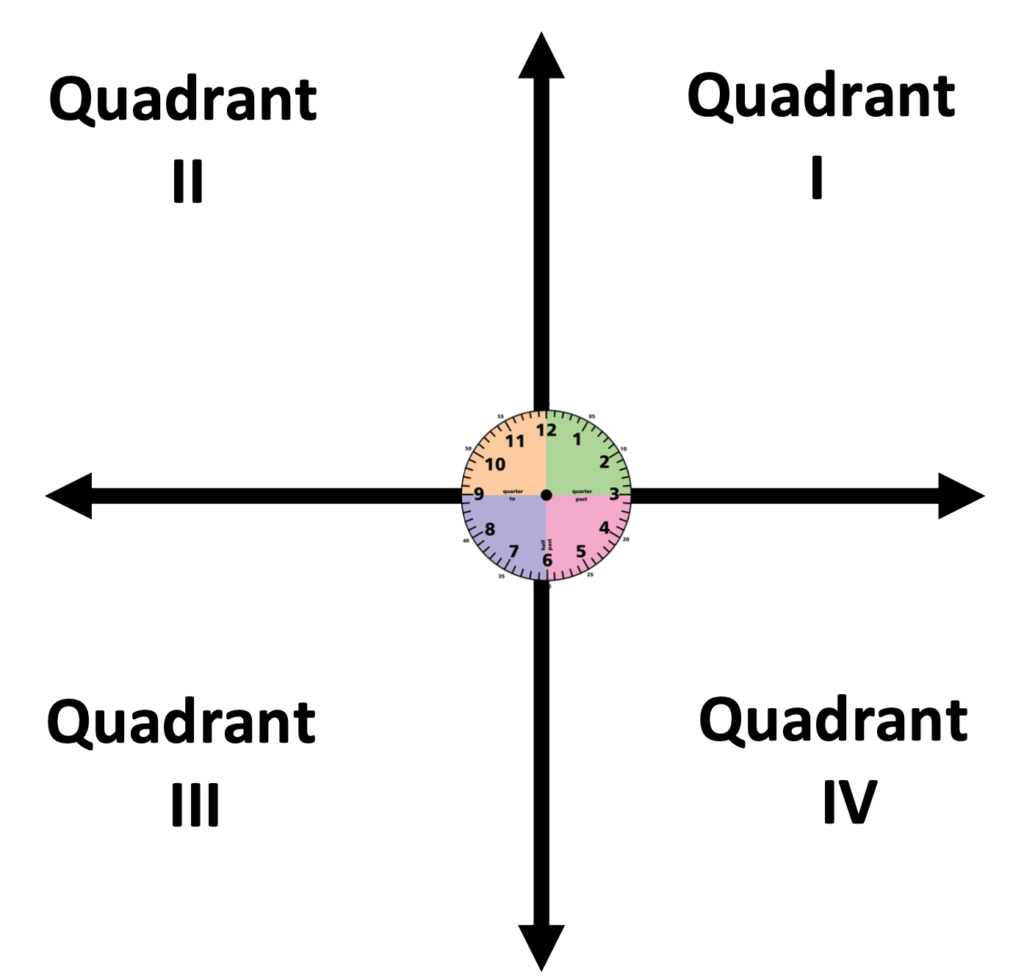
The X and Y Axis, and the Origin
Students with visual and reading comprehension challenges benefit significantly from color-coding words to images. Below you will find examples in which this is used to help students correlate words, directionality, and lines representing the x and y-axis.

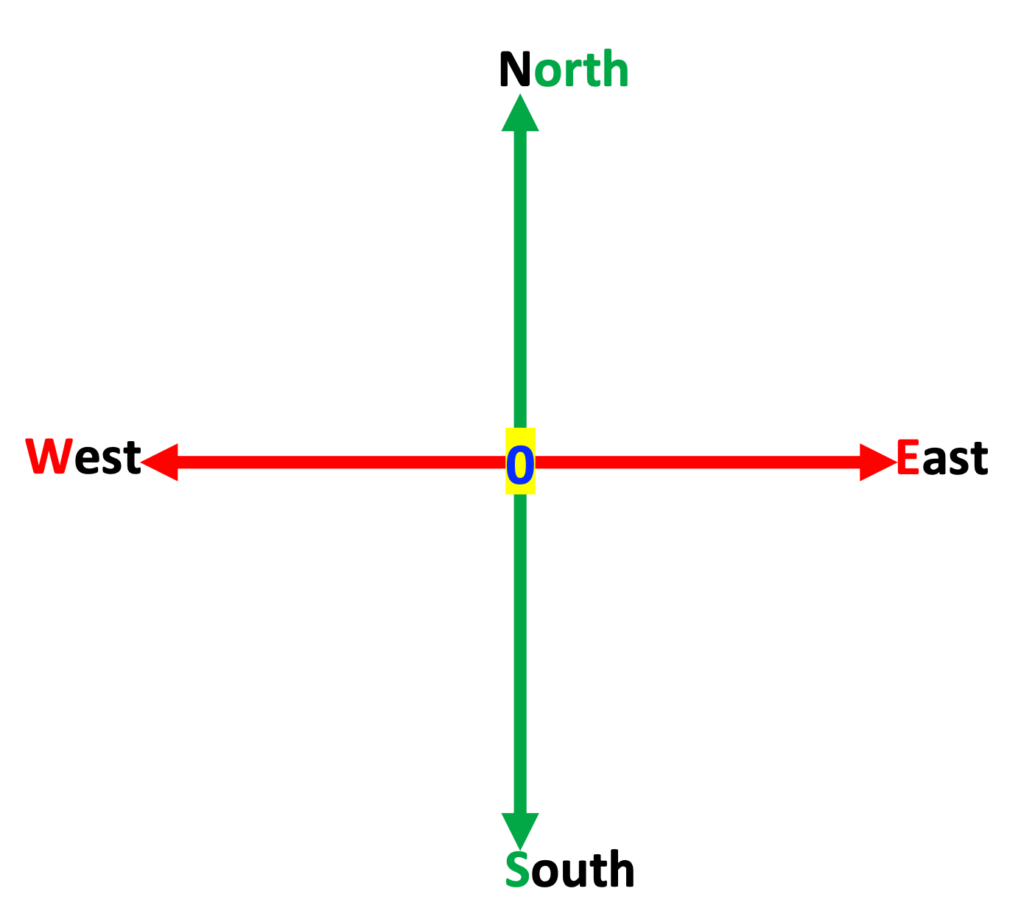
X: East and West, Y: North and South
Directional terms may also be understood through the use of real-life directions such as a weather vane, expressing directions for east, west, north, and south. A compass also uses these terms. I have found that the use of these terms has helped my students more easily relate to the x and y-axis.
Encourage students to come up with their own ideas for remembering each axis.
In the following example, note that I have also continued with the red and green to emphasize the x and y-axis. Carrying over the color of significant features helps students to continually make connections between concepts, promoting carryover from one concept to the next.

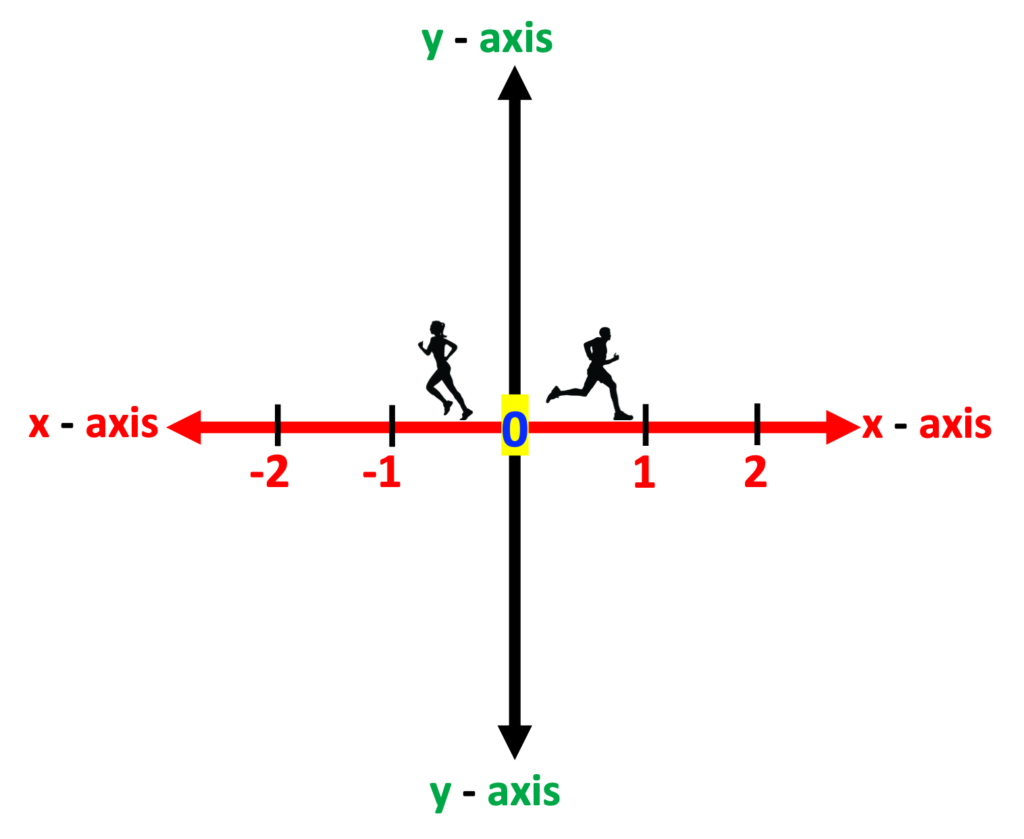
Numbers on the X-Axis
As you view the example below, notice that the y-axis line is black. I did this so that the x-axis would be more visually prominent. This allows students to visually focus on the x-axis without distraction from the y-axis. Also note that I placed two images of runners on the x-axis, going opposite directions from the origin. I love emphasizing this point in preparation for introducing slope, rise/run!
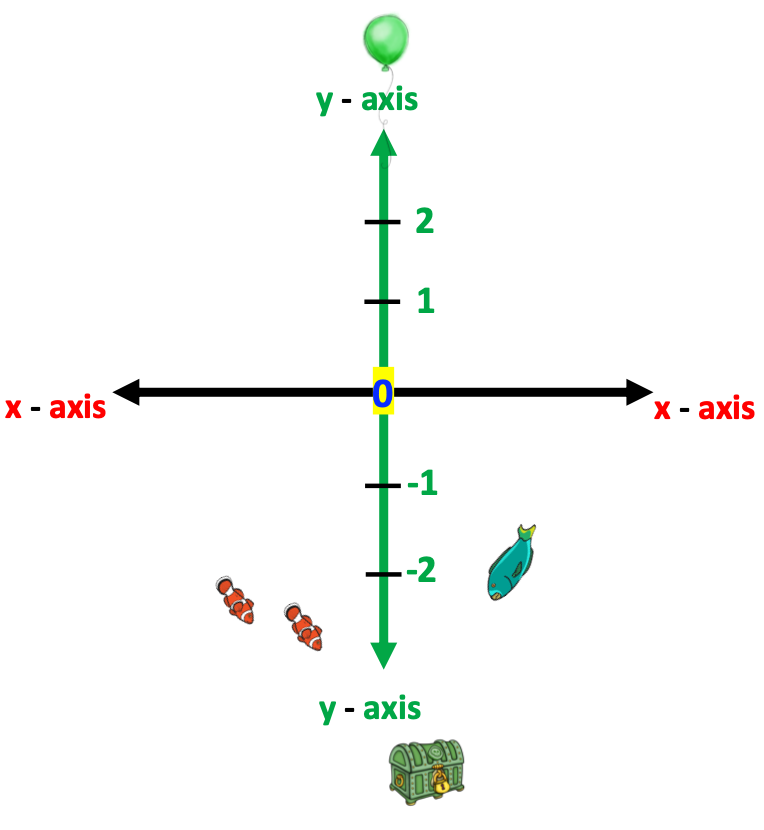
The y-axis is done, similarly.
Again, encourage students to come up with their own ideas.


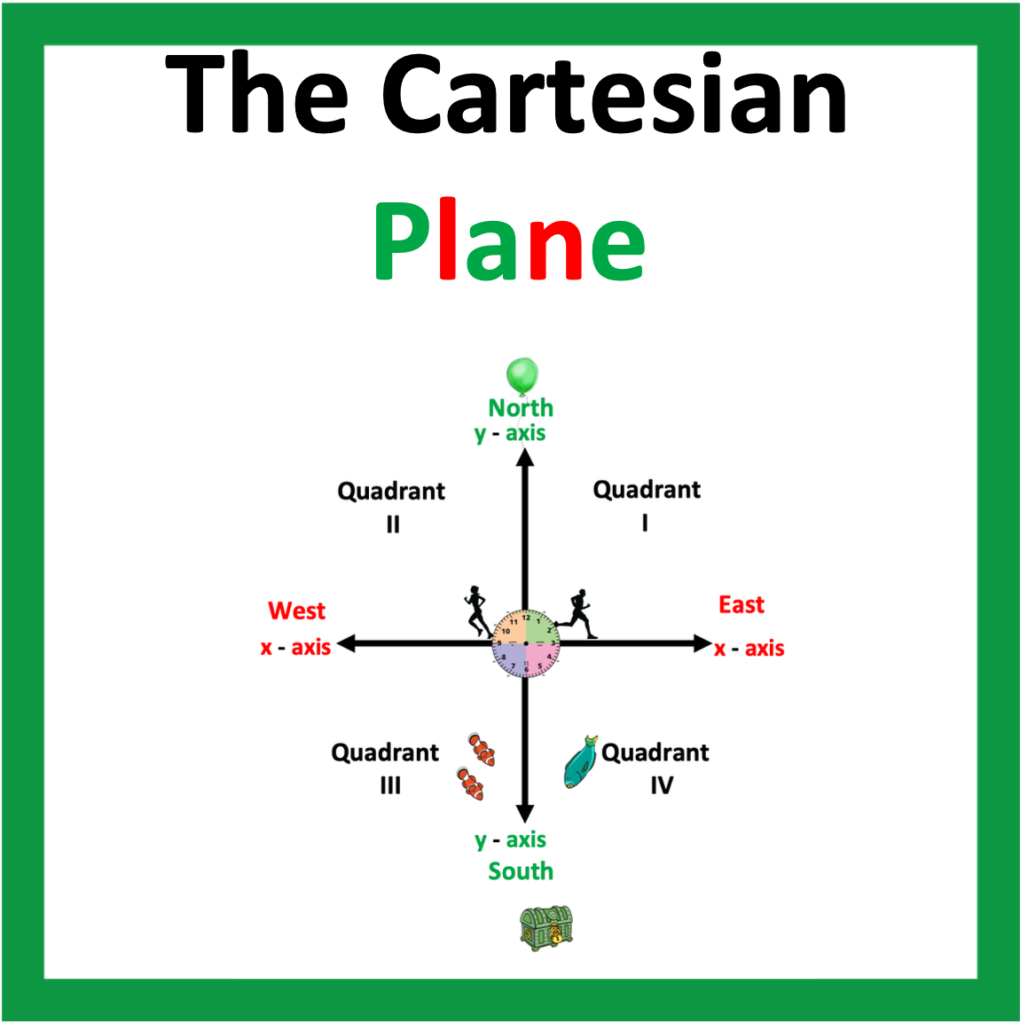
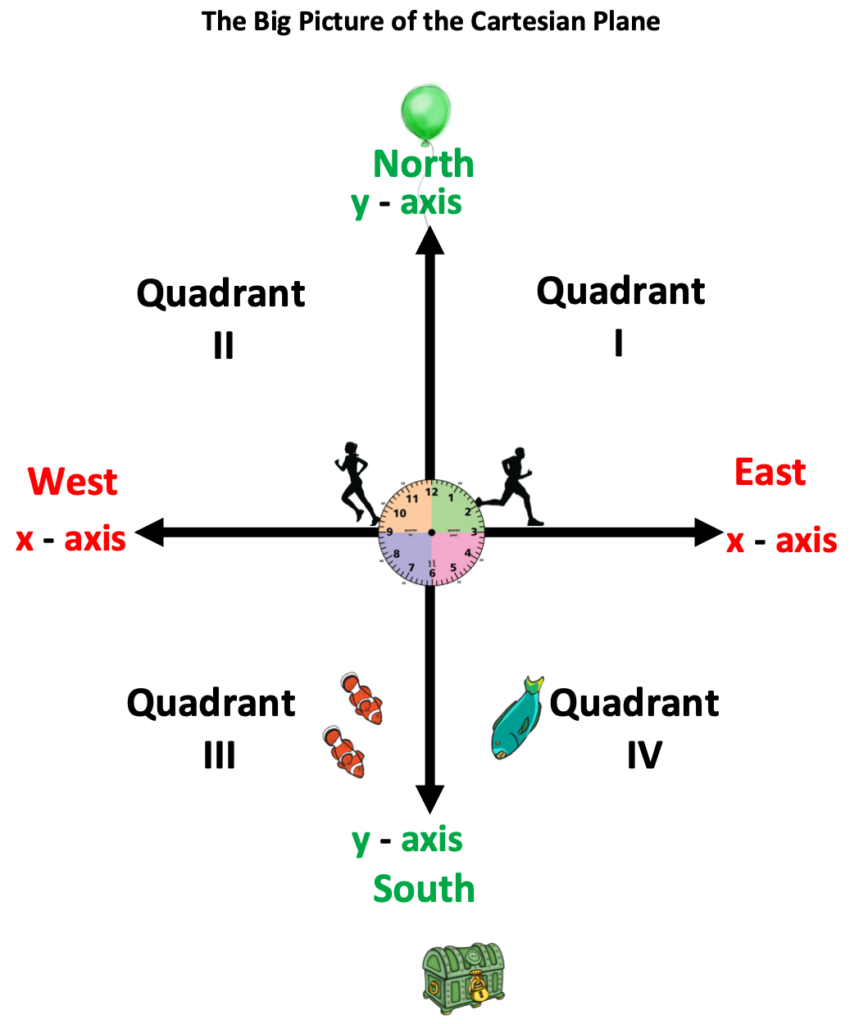
The Big Picture of the Cartesian Plane
Below is a combination illustration for the Cartesian Plane On this image you will note that each axis is black. This decreases the amount of detail, as too much color and contrast can also be visually overwhelming.
Below this image, you will find a product that may be purchased at my store. It contains these images and others, including a copy that is only in black and white, allowing students to add as much or as little color and illustrations.
Conclusion
By being aware of potential student challenges alongside strategies for intervention, students will be successful in graphing.
https://www.teacherspayteachers.com/Store/Bonnie-Stephan