You are teaching middle school math and have carefully prepared a lesson plan to teach multiplication of fractions. The lesson appears to have gone well.
On the other hand, when you review student homework the next day you notice errors related to basic math calculations. If this has ever happened to you, continue reading to learn how to successfully prepare students for fraction operations.
- Contents:
Introduction
1. Evaluate Basic Math Skills of Number Operations: Addition, Subtraction, Multiplying and Dividing
2. Provide Hands-On, Every-Day Activities that Involve Fraction Operations
3. Introduce the Numerator and Denominator
4. Use 10 x 10 Grids
5. Instruct Students How to Convert Between Mixed Numbers and Improper Fractions
6. Instruct Students How to List Factors of Numbers: Two Efficient Strategies
a. Number Patterns
b. Divisibility Rules
7. Instruct Students How to Find the Greatest Common Factor, GCF
8. Instruct Students How to Find the Least Common Multiple, LCM
Conclusion
1. Evaluate Basic Math Skills of Number Operations: Addition, Subtraction, Multiplication, and Division
By 5th grade you anticipate that most students will be able to complete at least 1 – 2 digit addition, subtraction, multiplication and division calculations with whole numbers.
On the other hand, it is ideal to do a quick check to determine what math calculations students may need to review as fractions include the same four operations. A quick check also helps when planning math groups in the classroom.
Also look to see if there are any students with an IEP (Individualized Education Plan) which may allow students to use a calculator with math tasks.
2. Provide Hands-On, Every-Day Activities that Involve Fractions
The emphasis should be placed on recognizing the difference between parts and the whole. Simple food preparation tasks are fun and multi-sensory! Such examples may include making pop-corn balls, granola, snack mix, and smoothies. Older students may enjoy making quick breads such as banana bread, biscuits or yeast breads.
The Process:
1. Introduce students to the measuring tools needed for a recipe:
teaspoon, table spoon, cup or use of a scale for measuring in ounces or grams
2. Discuss equivalency measures: 1 pint = 2 cups, and others.
Also, provide a nearby conversion poster for student reference.
3. Determine whether to decrease or increase the recipe.
Re-calculate the measures for each ingredient.
For example:
If decreasing the recipe by half, each measure must be divided by 2.
If increasing the recipe by three, each measure must be multiplied by 3.
When increasing the size of the recipe, some measures may result in the form of an improper fraction which will need to be converted into a mixed number.
Before measuring ingredients,
be sure ALL converted calculations
are accurate!


Likewise, chocolate bars which are divided into equal squares is also a tasty way to discover parts and the whole.
For example, if you have a candy bar with squares arranged in a 4 x 8 pattern, break the bar in half so there are two 4 x 4 squares. This means you now have two wholes, though the two wholes represent 4 x 4 chocolate squares or a total of 16 squares in each.
You may keep breaking up the candy bar until you cannot break it up any more. However, the fun is not over yet!
Next, do the reverse. Combine the 2 x 2 squares till the candy bar represents a whole.
While completing this activity, use descriptive words such as: part, whole, half, one-fourth, equivalent, equivalent fraction, adding, subtracting, dividing and multiplying and others.
Lastly, students may write a summary of the activity describing the fractions represented.
,
On the Side of Caution: Do be aware if there are students who have food allergies.
Also, be sure that you are the only person using cutting tools. To avoid the use of a knife, some foods may be cut in advance.

If food is not an option, items of different colors or categories may be used such as multi-colored paper-clips.
For example, if you have 6 paper clips, and 2 are blue = a fraction of 2/6, two represents the part and six represents the whole.
Also, encourage students to find other objects in the classroom that may be used to illustrate these concepts. The more examples with different objects, the better.
Furthermore, if you observe students squinting their eyes with question marks on their faces as you mention the words, “numerator” and “denominator,” these students may be silently trying to process what these terms mean but are too afraid to ask.
Keep reading.
3. Introduce the Numerator and Denominator
What a great time to discuss the numerator and denominator!
Do all your students know the difference between the numerator and the denominator?
Have you ever noticed that some students really struggle just pronouncing these words?
Below is an illustration to:
1. Help students learn how to pronounce these words.
2. Help students identify the difference between the “numerator” and “denominator”

4. Use 10 x 10 Grids
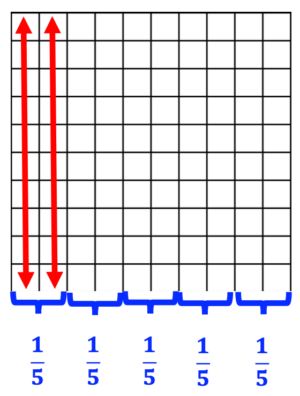
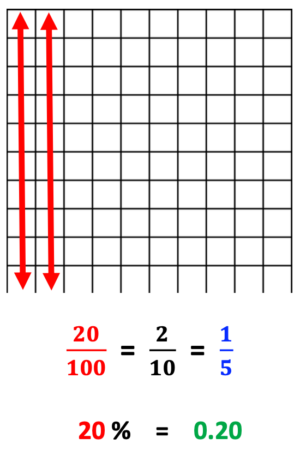
Use of 10 x 10 grids is a great way to provide visuals for fractions and create connections between fractions, decimals and percent. Observe the illustration below:
Notice the interesting connections between the illustration, fractions, decimals and percent:
1. Each grid has a total of 100 squares.
2. The red arrows cross 20 blocks out of 100 total blocks = 20/100.
20 / 100 reduced = 2/10.
2/10 completely reduced = 1/5.
20 out of 100 squares = decimal value of 0.20 = a percent value of 20 %
3. 1/5 + 1/5 + 1/5 + 1/5 + 1/5 = 5/5 = 1 whole = a decimal value of 1.00 = 100 %
1/5 of the blocks represent 20/100 blocks = a decimal value of 0.20 = 20 %
4/5 of the blocks represent 80/100 blocks = a decimal value of 0.80 = 80 %
1/5 + 4/5 of the blocks = a decimal value of 1.00 = 100 %
From the values above and the illustrations below, it is also easy to see the relationship between fractions, decimals and percent.
Class Activity
First: Place students in small groups.
Each small group is given a 10 x 10 grid and a fraction value.
Each group’s fraction value is different.
Second: Students illustrate the graph and list as many connections as possible that represent the value given.
Student groups take turns sharing their discoveries.
Third: Each presentation must include the following:
- Fraction value
- Decimal value
- Percent value
- Observed connections between the illustrated graph, fraction, decimal and percent.
To make the activity more challenging:
1. Give students a mixed number and more than one grid.
2. Give students numbers which go beyond the hundredths place.
Examples: 0.875, 0.625, 1/3, 2/11
Students may find the use of rulers useful, as students must come up with the most accurate grid application as possible.
Encourage creative thinking
5. Instruct Students How to Convert Between Mixed Numbers and Improper Fractions
Being able to convert between mixed numbers and improper fractions is an important skill to practice before learning fraction operations.
Below are illustrations for the following:
1. How to Turn a Mixed Number into an Improper Fraction
2. How to Turn an Improper Fraction into a Mixed Number


6. Instruct Students How to List Factors of Numbers: Two Efficient Strategies
How often have you observed students reducing fractions such as 16/24 by 2 until finally arriving at 1/6 when they could have used the greatest common factor of 4?
Providing strategies for listing factors is essential prior to students learning how to determine the greatest common factor. Confidence listing factors of numbers is a sure way to make this task much easier.
Furthermore, being able to list factors of numbers expands student ability to understand how numbers relate to each other.
Lastly, the ability to see how numbers relate to each other also provides a foundation for future math concepts covered in Algebra.
Number Patterns
Using number patterns is a great place to start.
For example, the number 88 can be broken in half.
Notice how the factors on the left double , whereas the numbers on the right, break in half.
Of course not all numbers break down as easily as 88, but the concept is very helpful with some even numbers.
88
1, 88
2, 44
4, 22
8, 11
Once my students discover such patterns, they marvel at how quickly they can list factors!
Divisibility Rules
On the other hand, how do students determine other factors of numbers?
Another strategy includes the use of divisibility rules.
The first set of factors students usually encounter are related to multiplication facts.
For example: 2 x 4 = 8
Two and four are the factors of the number, 8.
The number eight is described as the multiple of 2 and 4.
Yet another factor pair for 8 includes 1 and 8.
Below is a divisibility chart that is useful for finding factors of numbers. By using divisibility rules, students are able to quickly discover factors of a number and eliminate numbers that are not.

7. Instruct Students How to Find the Greatest Common Factor, GCF
After students understand what factors are, they are ready to list factors of two different numbers and find the greatest, or largest factor that both numbers share.
This skill is most helpful in reducing fractions.
Below you will find an example.

1. A fraction of 48/90 is given.
2. The factors for both 48 and 90 are listed.
3. Observe the factors of 48, as this number can be broken in half.
Also notice that 12 and 6, in addition to 4 and 8, can be split in half.
What is half of 16? 8
What is half of 6? 3
4. When comparing factors listed for 48 and 90, six is the greatest common factor.
5. To the right of the factor list, the greatest common factor of 6 is used to reduce 48/90 in one step.
8. Instruct Students How to Find the Least Common Multiple, LCM
Begin this concept two to four weeks before teaching addition and subtraction of fractions with unlike denominators.
I do not even mention adding and subtracting fractions with unlike denominators during this time as I want the students to only focus on listing numbers to determine the least common multiple. This allows students to learn a new skill without being overwhelmed by other details.
List the multiples from left to right, “Least goes East!”
Begin by giving students two numbers to list multiples for finding the least common multiple.
Next, give students three numbers to list multiples for finding the least common multiple.
Below is an example of listing multiples for 3 and 5.
3: 3, 6, 9, 12, 15
5: 5, 10, 15
15 is the least common multiple, the smallest multiple that both 3 and 5 share.
When students are confident finding the least common multiple, they are now ready to learn steps for adding and subtracting fractions with unlike denominators.
Also, when teaching fraction operations, leave adding and subtracting fractions with unlike denominators as the last operation.
Additionally, do you find that students often struggle identifying the difference between the greatest common factor and the least common multiple? Below are three solutions.
First, choose a time of the school year to teach each one. When school starts, provide practice opportunities for students to list factors of numbers 1 to at least 100. After students are confident listing factors, they may begin listing the greatest common factor between two numbers.
Second, the least common multiple is ideal to teach 2 – 4 weeks before introducing adding and subtracting fractions with unlike denominators.
Third: Remember to list multiples from left to right and factors from top to bottom. This method will help students “see” each list as different.
Conclusion
Just as you pack for a trip and ensure that all needed items are in your travel bags, preparing students with all the tools they will need prior to learning fraction operations is also essential.
A strong foundation in math concepts creates a pathway to fraction operation success!





