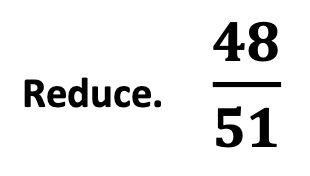You observe your students easily reduce fractions such as 4 / 6, 3 / 9 and even 25/75.
Next, your students encounter the fraction 51 / 87 and assume it is fully reduced.
Now what?
Looking for strategies that will provide success for these more challenging numbers?
If so, be sure to overview the easy to follow instructions which will greatly help students learn how to
reduce fractions.
- Contents:
1. Practice Listing Factors of Numbers to at Least 100- List Factors Vertically
- Use Divisibility Rules
- Observe Number Patterns
- Recall Multiplication Facts
- Last, Long Division
- Summary
- 2. Determine Common Factors
- 3. Determine the Greatest Common Factor, GCF
- 4. Reduce Fractions by Using the Greatest Common Factor, GCF
1. Practice Listing Factors of Numbers to at Least 100
Before ever beginning fraction operations I provide students with instruction how to easily list factors. Students may begin this process with small numbers when they learn multiplication facts. There are 4 approaches I have used that have been a game-changer for my students.
List Factors Vertically
First, teach students to list factors vertically, from top to bottom.

This format helps students distinguish between the listing of multiples and the listing of factors.
When listing multiples to find the Least Common Multiple for adding and subtracting fractions with un-like denominators, the multiples are listed from left to right.
LEAST GOES EAST!
Use Divisibility Rules
Second, when students are given larger numbers to break down, such as 87, an odd number, the use of divisibility rules are most helpful!
As I observe students listing factors of numbers and note that some factors are missing, I will provide a verbal cue such as,
“Did you test the number using all the divisibility rules?”
“I see that you have left the space under the numbers 51 and 87 blank.” I grin and add, “Go back and test the numbers using the divisibility rules.”
Below is a chart I give my students for testing divisibility to help discover factors of numbers.
DIVISIBILITY RULES FOR 2, 3, 6, 9, 5, 10, AND 11

If you are looking for practice worksheets which includes this chart, it can be found at:

https://www.teacherspayteachers.com/Store/Bonnie-Stephan
After listing factors vertically, you will always want to factor other numbers the same way!
This method can also be used with algebra concepts such as simplifying radicals and factoring polynomials.
Observe Number Patterns
Third, observe and get excited about number patterns! This has been by far my students’ most exciting discovery! After showing my students this strategy, the whole class echo’s their excitement with statements like,
“Wow! that is sooooooooo cool!”
“No way!”
“Awesome!”
As students begin to see that some numbers can be broken in half, they often discover factors that may not have been found with other methods.
In addition, as students use patterns, they may also discover factor pairs found using multiplication facts and divisibility rules.
These patterns are also included in the packet, “Discover Factors for Numbers Using Divisibility Rules,” as seen above.
Recall Multiplication Facts
Fourth, multiplication facts are useful for tricky numbers like 49 in which there are only two factor pairs:
1 x 49 and 7 x 7.
Last, Long Division
Sometimes students will find numbers that are divisible by 2 and 3 such as the number 78, though they are not aware of the other factors.
In this case, students may use long division.
Also check to see if the student has accommodations that allow for the use of a calculator for math calculations.
Below is an example of finding the factor pair for 30.
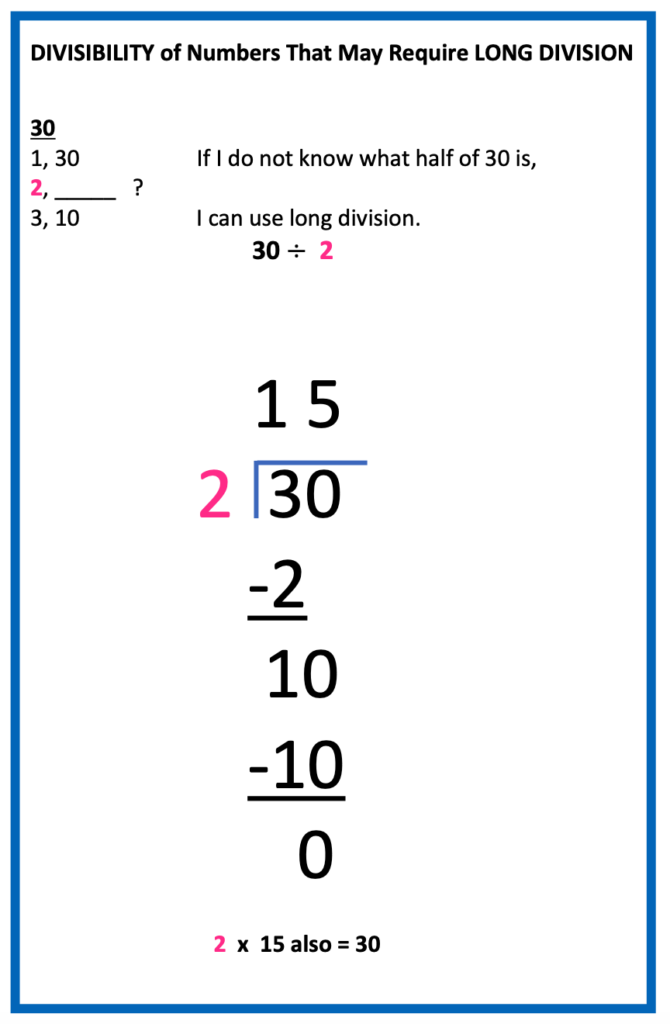
Summary: How to List Factors of Numbers
1. List Factors Vertically
2. Use Divisibility Rules
3. Observe for Number Patterns
4. Recall Multiplication Facts
5. Last, Long Division
2. Determine Common Factors
Once students begin to write factor pairs for individual numbers, they are soon ready to determine common factors that two numbers have in common. Below you can see that 2, 3, and 6 have been high-lighted as common factors that both 12 and 18 share.

3. Determine the Greatest Common Factor, GCF
After finding common factor pairs in the example above, find the greatest, largest number that both numbers share. The greatest common number would be 6.
4. Reduce Fractions by Using the Greatest Common Factor, GCF
Let’s look at an example of a fraction that can be reduced.
Now you can see how this method will prepare students to successfully reduce fractions.

Conclusion
The ability to successfully reduce fractions stems from the ability to list factors of numbers, which in turn provides a direct pathway to most efficiently finding the greatest common factor. Next, the GCF is used to reduce both the numerator and denominator in one quick step.
Hurrah!!!