The school year has started. As you reflect on the year before, you plan to make this year the best year ever! Your goal: to successfully teach fraction operations!
Your preparation begins with a new internet search. However, the more you look, the more overwhelmed you feel as you observe so many different methods!
I’ve been there and know how you feel. This lead me to determine the most efficient and effective ways to teach fraction operations! I encourage you to keep reading as you will discover strategies, resources and materials that will pay off big!

Contents:
- 1. Introduction
2. Preparation Begins on the First Day of School
3. General Recommendations for Successfully Teaching Fraction Operations- The Horizontal Method
- Use Proper and Improper Fractions
- Introduce Fraction Operations that Result in Reduced Form
- 4. Teach Fraction Operations in a Specific Order
- Week 1: Add and Subtract Fractions with Like Denominators
- Week 2: Multiply Fractions
- Week 3: Divide Fractions
Week 4 – 5: The Least Common Multiple
Week 6 – 7: Add and Subtract Fractions with Unlike Denominators
- 5. Conclusion
Preparation Begins on the First Day of School
Yes! Fraction preparation begins on the first day of school or whenever you are reading this! You will discover that the following preparation methods will serve as a solid foundation for fraction operations.
Where to Start
1. Evaluate student abilities to complete basic math calculations: addition, subtraction, multiplication and division.
2. Provide extra instruction and practice for basic math calculations as needed.
3. Provide instruction and practice listing factors of numbers 0 to at least 100.
Elementary level students may begin this concept by practicing fact families via puzzles and worksheets.
Listing factors of numbers will prepare students to find the greatest common factor, a stepping stone for reducing fractions.
4. Begin collecting instructional resources and materials that provide a logical, easy-to-follow approach.
While sifting through multiple approaches, resources and materials, I decided to venture out and create my own approach for teaching fractions. It has proved both efficient and effective for all students.
At the end of this article, you will find my materials listed and available for your use.
General Recommendations to Successfully Teach Fraction Operations
The Horizontal Method vs. Vertical Method
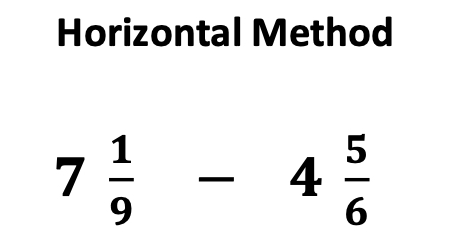
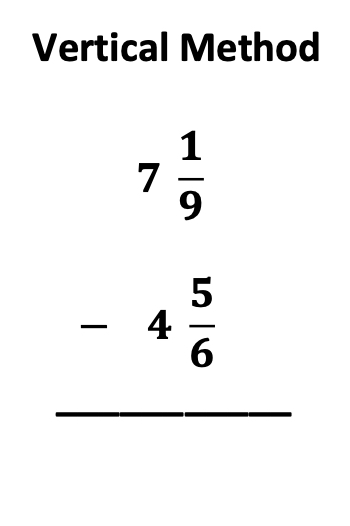
You may have seen fraction problems in both vertical and horizontal forms as described above. Does it matter which method is used?
While reviewing fraction operations with a small group of Algebra students, a student looked at me like I had lost my mind as she interjected,
“What do you mean I need to solve fraction problems from left to right! I’ve always stacked them like this and I don’t understand why I have to change that now!”
Wow. I was a bit taken back with her tone and adamant spirit. Given this, I could clearly sense her frustration.
So does it matter which method is used from the very beginning? You bet it does!
Yes. As early as fraction operations are taught, I highly recommend that the horizontal method be used for all fraction operations.
Use Proper and Improper Fractions

When introducing students to fraction operations, begin with proper and improper fractions only!
Why?
When using mixed numbers, students must learn additional steps to solve fraction operations. Using only proper and improper fractions for each operation help students focus on the specific steps of the operation being taught.
On the other hand, what if your math curriculum has combined proper, improper and mixed numbers for instruction and practice?
No problem.
After students are confident with addition, subtraction, multiplying and dividing fractions, these pages may be added.
Introduce Fraction Operations that Result in a Reduced Form
In addition to using only proper and improper fractions, select fraction problems that cannot be reduced. Once again, focus on the unique steps for each type of fraction operation.
However, from the the beginning of the year, prepare students for reducing fractions using the listed order below.
1st: Review basic multiplication and division facts
2nd: Practice listing factors for numbers 0 to at least 100
3rd: Practice finding the greatest common factor
First, ensure students are confident with basic multiplication and division facts. This skill provides students tools to use when listing factors. Once students are able to list factors of numbers, finding the greatest common factor is completed with ease. Students are now equipped to successfully reduce fractions with both small and large numbers.
Likewise, the ability to list factors is paramount for middle school math and high school algebra.
Teach Fraction Operations in a Specific Order
Week 1: Add and Subtract Fractions with Like Denominators
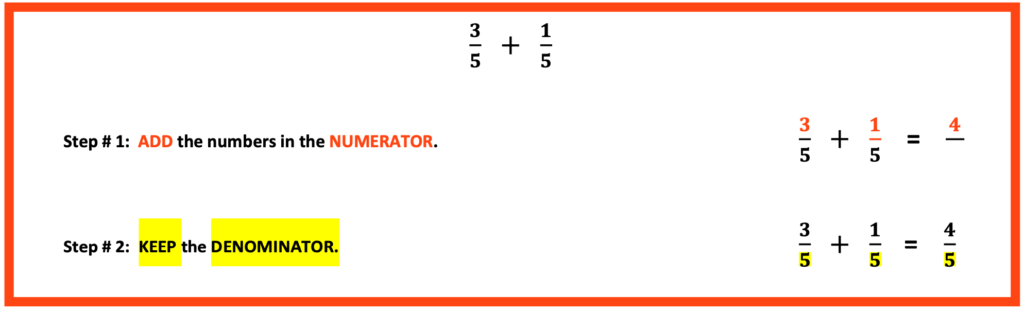
Above is an illustrated example for adding fractions with like denominators.
1. Add the numbers in the numerator
2. Keep the number that is in the denominator
The operations for subtracting fractions will be similar:
1. Subtract the numbers in the numerator.
2. Keep the number that is in the denominator.
Example: 4/5 – 1/5 = 3/ 5
Why start with addition and subtraction of fractions with like denominators?
1st: Students are likely to be most confident with addition and subtraction.
2nd: Addition and subtraction of fractions is easily illustrated with blocks, pie pictures or other hands-on-objects. The number in the numerator can be represented as the parts and the number in the denominator as the whole.
3rd: Addition and subtraction of fractions require only two steps.
After introducing addition and subtraction of like denominators, provide a daily review.
Week 2: Multiply Fractions

1st: Multiply the numbers in the numerator from left to right.
2nd: Multiply the numbers in the denominator from left to right.
Students may benefit from drawing arrows from left to right.
Review:
1. addition and subtraction of fractions with like denominators
2. multiplication of fractions
3. Provide mixed practice for addition/subtraction with like denominators and multiplication of fractions. This provides students opportunity to practice distinguishing between the unique characteristics of fraction operations.
Week 3: Divide Fractions
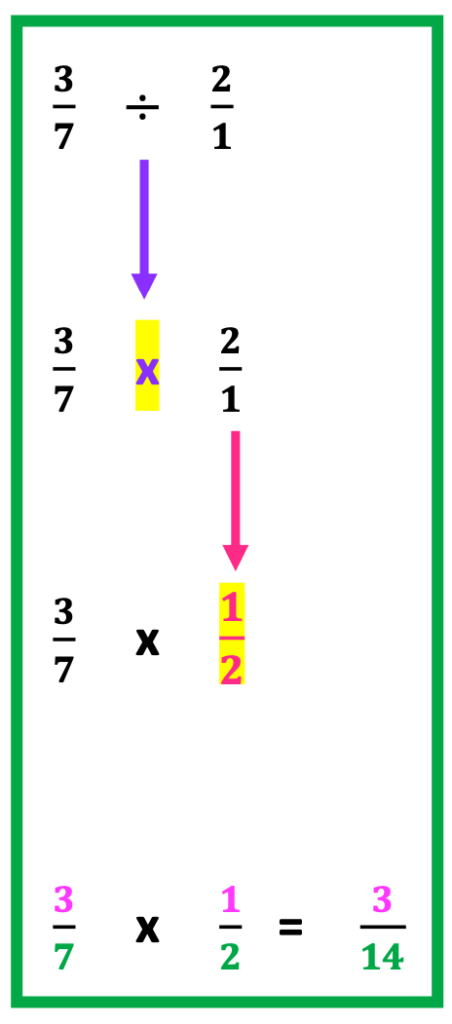
Once students understand how to multiply fractions they are well equipped to learn steps for dividing fractions.
1. Help students identify two terms in the problem. In the above illustration, 3/7 is the first term and 2/1 is the second term.
2. Keep the first term, 3/7.
3. Change the division sign to a multiplication sign.
4. Flip the last term, 2/1.
5. Solve by multiplying numbers from left to right. When students learn how to multiply fractions before dividing fractions, this step will feel familiar.
3 x 1 = 3
7 x 2 = 14.
The final answer = 3/14
Review:
1. addition and subtraction of fractions with like denominators
2. multiplication of fractions
3. division of fractions
4. Provide mixed practice for addition/subtraction with like denominators, multiplication and division of fractions. This provides students opportunity to practice distinguishing between the unique characteristics of fraction operations.
Week 4 – 5: The Least Common Multiple, the L.C.M.

At least two weeks
before teaching
addition and subtraction of fractions
with unlike denominators,
introduce students
to steps
for finding the L.C.M.
The Process:
1. Teach students what multiples are.
2. Use the Step Method to determine the least common multiple.
3. Practice finding multiples of numbers.
First, find the L.C.M. for a set two numbers.
Second, to increase the challenge, find the L.C.M. for a set of three numbers.
For example:
Given 2 sets of numbers, find the L.C.M for 2 and 3.
2: 2, 4, 6
3: 3, 6,
The L.C.M. is 6
Given 3 sets of numbers, find the L.C.M for 2, 7, and 14.
2: 2, 4, 6, 8, 10, 12, 14
7: 7, 14
14: 14
The L.C.M. is 14
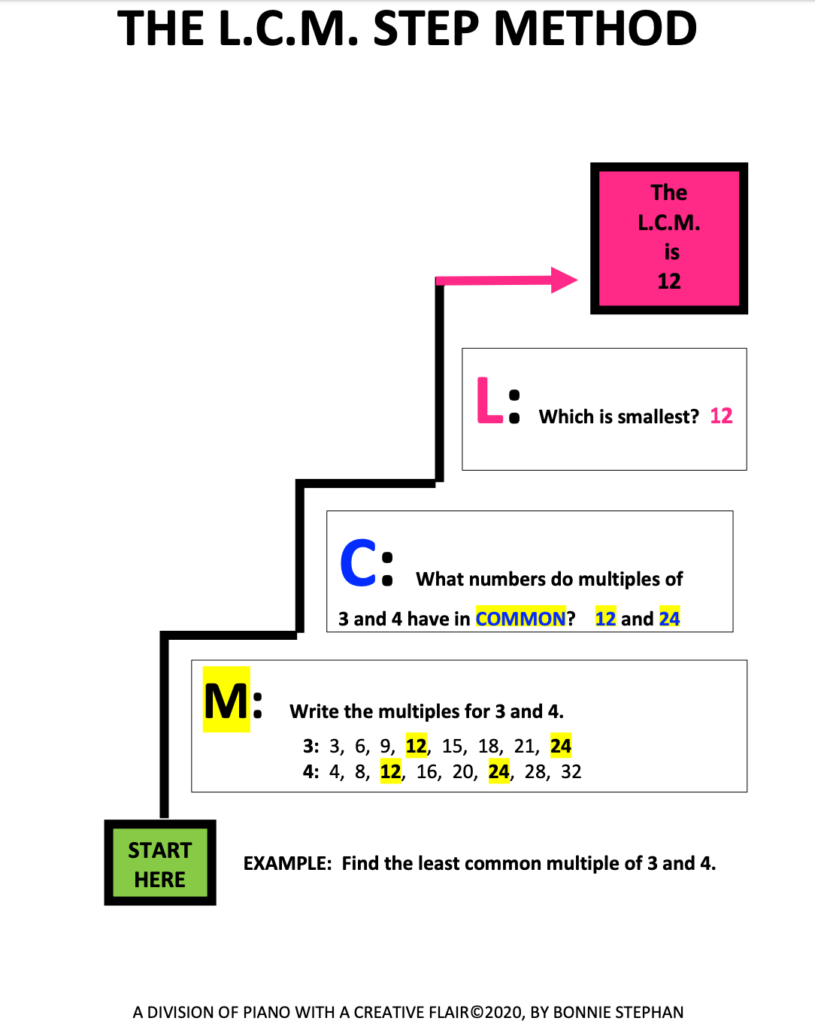
Quick Tips for Listing the Multiples of More than One Number:
1st: List 3 – 5 multiples of the largest number.
2nd: List 3 – 5 multiples of the smallest number
If three numbers are given, list 3 – 5 multiples of the other number.
3rd: Repeat if the greatest common multiple has not been found.
Provide daily practice for finding the least common multiple.
Review:
1. addition and subtraction of fractions with like denominators
2. multiplication of fractions
3. division of fractions
4. Provide mixed practice for addition/subtraction with like denominators, multiplication and division of fractions. This provides students opportunity to practice distinguishing between the unique characteristics of fraction operations.
Comprehensive review and practice of all fraction operations learned up to this point is critical prior to introducing addition and subtraction of fractions with un-like denominators.
Week 6 – 7: Add and Subtract Fractions with Unlike Denominators
Congratulations!
Your students are ready!
You are ready!
Let’s do this!
Observe the detailed step-by-step example below:

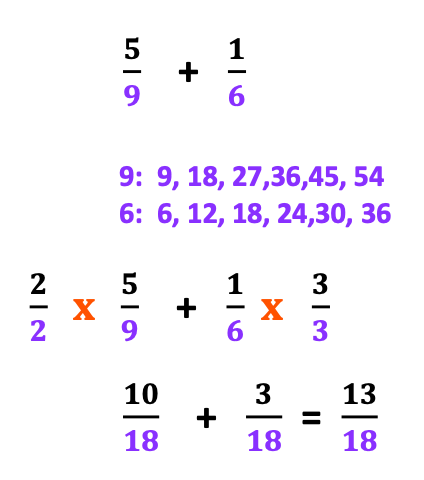
Note that the first step requires students to find the least common multiple, a step practiced the past two weeks. Such preparation provides a smooth transition allowing students to absorb the remaining steps for adding and subtracting fractions with unlike denominators.
Creating like denominators is a new step. The goal in this step is to create 20 as the denominator for both fractions.
This is accomplished by multiplying the numerator and denominator of each fraction by a fraction that will yield the least common multiple of 20 in the denominator of both fractions.
For example, the fraction 3/5 must be multiplied by 4/4, as 4/4 x 3/5 will result in 12/20.
Likewise, the fraction 1/4 must be multiplied by 5/5, as 1/4 x 5/5 will result in 5/20
Both fractions now have a denominator of 20.
Wow! We have gone full circle with fractions. The third step: Add fractions with like denominators!
12/20 + 5/20 = 17/ 20
You did it!!! Hurrah!!!
For your fraction enjoyment, below is another example.
Review:
1. addition and subtraction of fractions with like denominators
2. multiplication of fractions
3. division of fractions
4. least common multiple
5. addition and subtraction of fractions with unlike denominators
6. Provide mixed practice for all fraction operations. This provides students opportunity to practice distinguishing between the unique characteristics of fraction operations.
Furthermore, comprehensive review and practice of all fraction operations to the end of the year will greatly increase student ability to retain memory of fraction operations.
Always be looking for different types of math applications where fraction operations can be included for further practice. Below are ideas.
1. Geometry: finding measurements such as perimeter, area, surface area and volume of objects
2. Statistics: Determining the probability of events
3. Construction projects: building models, re-sizing using ratios to compare measures of the original/actual size and model size
4. Design costumes which require detailed measurements
5. Enlarge or decrease measures of a recipe
6. Create a book, power point, or video which describes how to complete fraction operations.
a. create models illustrating fraction problems
b. list daily applications of fractions and why the use of fractions is important
c. write poetry / songs pertaining to steps used to complete fraction operations
d. describe occupations that must use fraction operations, describing specific examples: carpentry, plumbing, nursing, pharmacy, and others
Conclusion

Student success with fractions is the result of careful planning and year-long practice of review from one year to the next.
Furthermore, fraction operations are more than just a check-off on the lesson plan. Fractions and their applications to science and higher-level math are ongoing. Believe me when I say algebra teachers will thank you!
Always remember that you are part of the solution!
For your convenience, click the blue box below to find resources and materials to help you succeed in teaching fraction operations. Below the blue box are the titles of materials you will find at my store.