How to Successfully Teach Fraction Operations

You are preparing lesson plans to teach fraction operations; multiplying, dividing, adding and subtracting with like and unlike denominators. You search the internet in hopes of a magical method that may make sense to your students. However, the more you look, the more overwhelmed you feel by the multiple methods used. I’ve been there and know how you feel. I’ve got you covered with common sense methods that will make this year the best ever! Keep reading to discover how to successfully teach fraction operations.

Outline:

• Teach All Fraction Methods Using the Horizontal Method
• Introduce all Operations Using Only Proper and Improper Fractions Before Mixed Numbers
• Introduce Fraction Operations that Always Result in Answers that are in Reduced Form
• Teach Fraction Operations in the Following Order
  • Before and while teaching fraction operations, provide daily practice listing factors of numbers from 1 – 100.
    • Week 1: Adding and Subtracting Fractions with Like Denominators
    • Week 2: Multiplying Fractions
      • Review Adding and Subtracting Fractions with Like Denominators
    • Week 3: Dividing Fractions
      • Review Adding and Subtracting Fractions with Like Denominators and Multiplying Fractions
    • Week 4 – 5: Teach the Least Common Denominator, LCM with No Reference to Adding and Subtracting Fractions with Unlike Denominators
      • Review Adding and Subtracting Fractions with Like Denominators, Multiplying and Dividing Fractions
    • Week 6 – 7: Teach Adding and Subtracting Fractions with Unlike Denominators Using the Least Common Multiple
      • Review Adding and Subtracting Fractions with Like Denominators, Multiplying Fractions and Dividing Fractions

If you need a motivating reason to use methods that you will learn in this blog. let me share that these basic methods for all operations occur again in Algebra, Geometry, and Statistics.

By making fraction operations a breeze to learn and remember from year to year in Middle School, what awesome success students will have in high school! And might I add, how relieved and grateful will be the their teachers!

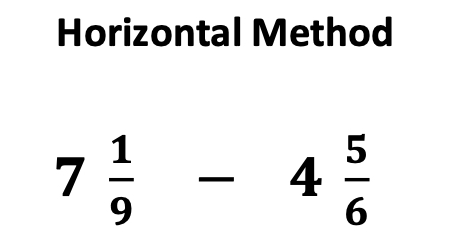
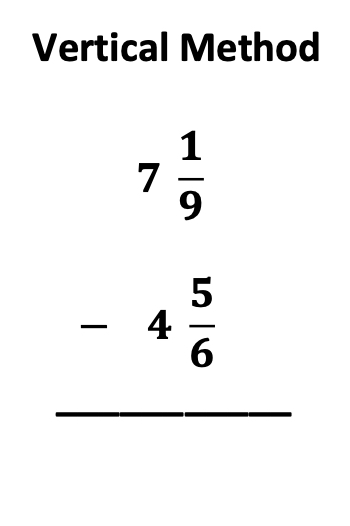
Maybe you have seen fraction problems in both vertical and horizontal form. If you have taught both forms, I am guessing that students may have experienced confusion as they went on to middle and high school. So true in my experience as you will see in the story below.

In the small group I taught, there was an Algebra 1 student I had never worked with before. We were reviewing fraction operations when the student looked at me like I had lost my mind.

“What do you mean I need to solve fraction problems from left to right! I’ve always stacked them like this, and this is the way I learned them. I don’t understand why I have to do it differently now!”

Wow. I was a bit taken back with her determined comments. Bless her heart, I could sense her frustration.

From this experience I only became more determined to emphasize the importance of teaching fractions at any grade level from left to right, horizontally. Fortunately, as I have been reviewing materials and curriculums that teach fractions, I am observing that more are teaching fractions in horizontal form, even when they are first introduced. What a relief for students and teachers!

Yes. As early as elementary school, I recommend teaching fractions from left to right, horizontally. Believe me, it will decrease student confusion both now and later.

The goal when teaching fractions is to make each type of fraction operation easy to learn. I have found that using only proper and improper fractions for each operation has really helped my students successfully, and more consistently determine the different rules between operations. Truly a game changer.

What to do if your curriculum has combined proper, improper, and mixed numbers for instruction and practice? No problem. The pages in your given curriculum may be used as extra practice after students are confident in adding, subtracting, multiplying and dividing fractions after they are confident solving proper and improper fraction operations. However, when teaching the basic operations, provide students with downloadable materials that provide this option.

So what to use for instruction? Detailed, step by step, color-coded directions work best. You will find specific detailed lessons, puzzles, and posters for multiplying, dividing, and adding, subtracting (like and un-like) denominators at my store that may be purchased individually or as a bundle. See the link below to find these and other helpful products.

https://www.teacherspayteachers.com/Store/Bonnie-Stephan

One of my favorite free sites that provide these materials is: Worksheet Works, https://www.worksheetworks.com/. After clicking this link, you can look through the math section and select fractions, or just directly click https://www.worksheetworks.com/math/fractions.html. From there you will look further down the page and find a section entitled, “Fraction Operations” in which you may choose the specific operations you would like students to review. As you continue to click, you will be able to create a fraction worksheet specific to what you are looking for.

• Though I do like this site for downloading worksheets for practice, I do need to mention that the answer pages may show a different method for completing each problem. Just use the answer sheet to check student answers. If students get a problem wrong, explain it using the same method taught in my lesson materials.

In addition to using only proper and improper fractions for fraction operation instruction, I also select fraction problems that cannot be reduced. Once again, focusing on the unique steps for each type of fraction operation is key.

To prepare students for reducing, provide materials that re-enforce the basic multiplication facts 0 – 9 or higher. The practice of listing factors for numbers 1 – 100 is also helpful.

Before and while teaching fraction operations with proper and improper fractions, provide daily practice reviewing multiplication facts and listing factors of numbers from 1 – 100.

As students practice multiplication and writing factors of numbers, their ability to find the greatest common factor, GCF, will flow naturally. This will provide student confidence when reducing fractions is introduced.

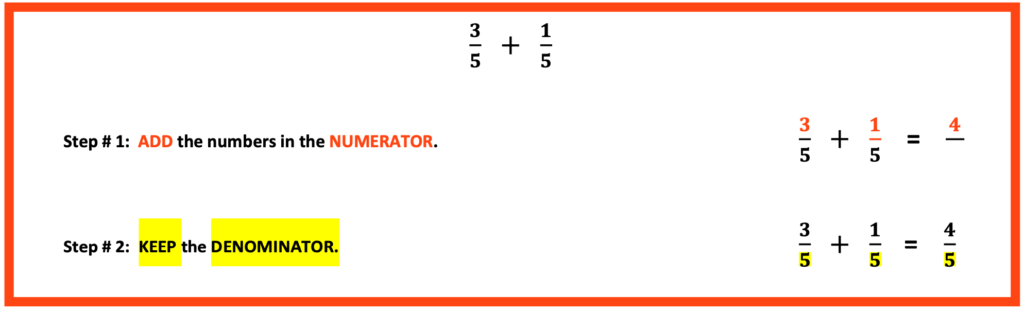
Week 1: Adding and Subtracting Fractions with Like Denominators

Start with adding and subtracting fractions with unlike denominators.

Why?

First, these concepts can easily be illustrated by blocks, pie pictures or other hands-on objects. First, when students understand that the number in the bottom (the denominator) represents the whole and that the whole does not change, they are able to understand why we keep the bottom number (the denominator). Likewise, if we add or take parts away, students can see that the number that changes is the top number (the numerator). Second, teaching this operation first, only requires only two steps:

1. Add or subtract numbers in the top (the numerator).
2. Keep the number in the bottom (the denominator).

Continue to practice writing factors for numbers 1 – 100.

Week 2: Multiplying Fractions

Before beginning multiplication of fractions, review adding and subtracting fractions to check for student understanding. Also be aware if there are students who need supports for multiplication.

Next, teach multiplication of fractions working from left to right, horizontally for both the numbers in the top (numerator) and in the bottom (numbers in the denominator).

• 1. Multiply the numbers from left to right in the top (numbers in the numerator).
• 2. Multiply numbers from the left to right in the bottom (numbers in the denominator).
• Encourage students to draw arrows from left to right from one number in the top to the next number in the top.
  • Repeat the same process with the numbers in the bottom, (denominator)
    • Drawing arrows from left to right is great for students who struggle with sense of direction, as they can feel and see the direction they are going.
• 3. Continue to practice writing factors for numbers 1 – 100.
• 4. Continue to review adding and subtracting fractions with like denominators.
  • To change practice up a bit, include word problems with the same types of fractions.
• 5. Include word problems for more practice and challenge.

Why I do not use the cross-cancel method for multiplication.

First, I want students to be able to take any fraction answer no matter the size and determine if it can be reduced by using skills they have learned when factoring numbers 1 – 100. Students can then easily see whether there is a GCF and then proceed to reduce the fraction to lowest terms. How often have you observed students reducing a fraction such as 66/88 by 2 until it will no longer reduce by 2.

How often have you observed students reducing a fraction such as 66/88 by 2

until it will no longer reduce by 2?

Second, some of my students, cross-cancelling can get pretty messy to the point that students cannot see what they have left to cancel or they lose track of what number cancelled with which number.

PHOTO of a messy cross cancel

Week 3: Dividing Fractions

Once again, check student understanding for adding and subtracting fractions with like denominators and multiplication of fractions.

Continue to provide review for adding and subtracting fractions with like denominators and multiplication of fractions.

Yes. Mix it up with related word problems.

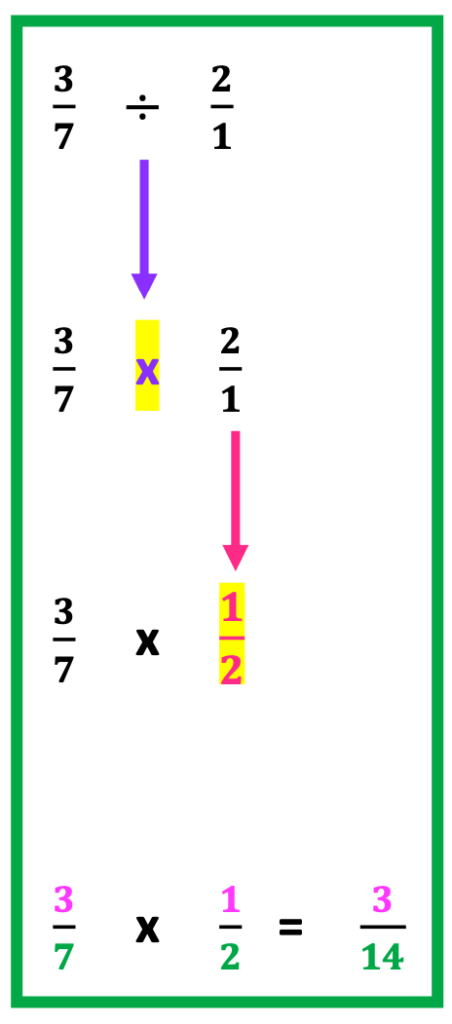
Once students understand how to multiply fractions, learning to divide fractions is much easier.

A method for division of fractions includes the “Keep” “Change” “Flip” method. It is a method I advocate as it is straight forward and easy for students to understand and remember when illustrated as seen in the green box above.

Week 4 – 5: Teach the Least Common Denominator, LCM with No Reference to Adding and Subtracting Fractions with Unlike Denominators

VERY IMPORTANT!

The best time to teach the

LeastCommon Multiple, the LCM,

is 1 – 2 weeks

PRIOR to teaching students

how to add and subtract fractions with

UN-LIKE DENOMINATORS!

However, there are curriculums that introduce the least common multiple, the LCM,

and the greatest common factor, the GCF, at the same time.

If possible, avoid teaching these concepts at the same time.

Students will best make sense of the LCM

when students are able to use the LCM,

such as when adding and subtracting fractions with un-like denominators.

Weeks 4 – 5 is a good time to make sure that students are able to continue review of adding and subtracting fractions with like denominators, multiplying and dividing fractions. Having a solid foundation in these first three operations is paramount prior to teaching adding and subtracting fractions with unlike denominators.

The concept of the least common multiple, the LCM, in itself is not difficult, though can cause some students stress if both are taught at the same time without ample practice on this skill alone.

Key points about the Least Common Multiple

1. Listing the least common multiple is similar to skip counting. Example: Skip counting for 3 = 3, 6, 9, 12, 15, 18 …
2. When listing multiples, I write each number going from the left to the right. I further explain this by saying: “LEAST goes EAST”.
3. I also mention the steps for finding the least common multiple as follows:

Step 1: List Multiples for Two Numbers such as 3 and 4.

3: 3, 6, 9, 8, 12, 15, 24

4: 4, 8, 12, 16, 20, 24

Step 2: What multiples are in common with 12 and 24?

Step 3: What is the least, smallest number they both share? 12

12 is the least common multiple, LCM

A Common Challenge

When students begin learning how to list numbers to find the least common multiple, they will often list a mile long list of multiples for the first and the second number.

How to Find Multiples Quickly:

1. List 5 multiples for the first number
2. List 5 multiples for the second number
3. Check and see if there are any common multiples between the two numbers. If there are, stop there.
4. If there are no common multiples, list 5 more multiples for each number and then check for any common multiples.
5. Repeat this process until a least common multiple is found.

After students are confident finding the least common multiple for two numbers, use the same steps for finding the LCM for three or more different numbers in the denominator.

Week 6 – 7: Teach Adding and Subtracting Fractions with Unlike Denominators Using the Least Common Multiple

• Continue to review all fraction operations learned up to this point.
• Adding and subtracting fractions with unlike denominators is last. So far students have been taught all other operations up to this point. Next, they will apply many of the concepts they have learned from other fraction operations as well as a couple new steps. See the examples below: