How to Use Number Lines with Inequality Math Statements
Do your students struggle with math inequality statements and number lines? Are you looking for strategies that will help students understand the relationship between the two? Keep reading. In this post, learn how to use number lines for inequalities to help students discover solutions.
#1 – Review Inequality Symbols in Elementary School
You have your lesson plan in front of you, “Number lines with Inequality Math Statements” and only minutes after you have begun, you discover some students do not know the difference between greater than or less than. Yes. This is a great time to provide examples for using inequality signs.
Though students will be introduced to the equal, less-than, and greater-then signs, they do not always remember how to interpret the signs.
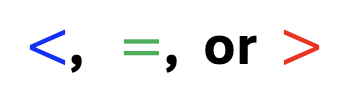
And for the most part, such problems have been focused on comparing numbers such as the below examples.


Students need to know how to read these symbols. This will help increase student confidence when learning more about inequalities and special features on the number line.
To learn more about inequality strategies for elementary students, visit to the following post:
How to Introduce Inequality Symbols in Math. Click on the link below.
#2 – Explore Number Lines
Also, as math teachers we are always looking for every-day examples to explain math concepts. This is what helps our kids understand symbols and other concepts in math.
When I explain a number line, I look for everyday common examples. Some of my favorites include temperature, money, height, width, volume, animals and food.
When it comes to the type of number line, vertical vs. horizontal, I find that both work well for certain types of problems. For example, I like to begin by comparing a thermometer to a horizontal number line. Students can relate to a rise and fall of temperature. It also works for illustrating the measurement related to the rise and fall of rivers.
Also, both inequality signs and graphing can be applied in student environmental science reports; math applied to science! How awesome is that?
A. Examples of Vertical Number Lines Using Temperature
Now that you have reviewed inequality signs, your students are ready to learn about inequality statements and the related graphs.
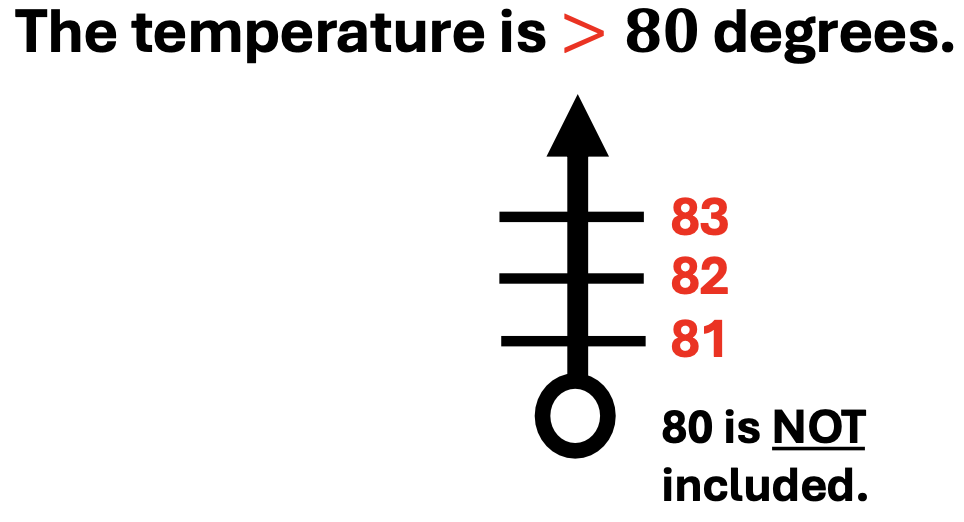
Below is an example of an inequality statement with a vertical number line. Notice the following:
1. The greater-than sign is color-coded to match the numbers that make the statement true.
This includes all temperatures above, GREATER THAN 80 degrees.
Color-coding helps students visualize the relationships between the symbols and numbers.
2. The circle at the bottom of the number line is not filled in at the 80 mark.
This means that a temperature of 80 degrees is NOT included.
It also means that all temperature values above 80, will make the inequality statement true.
The more examples you provide, the more students will grasp these concepts.
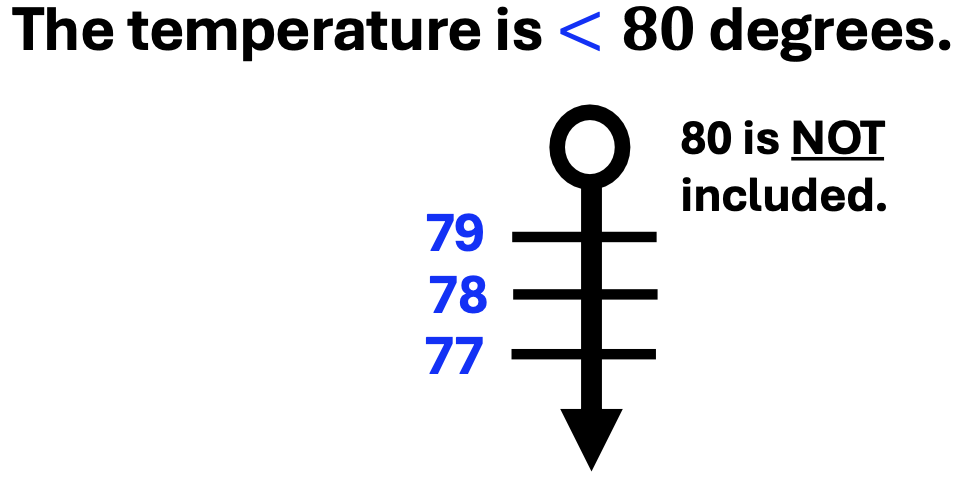
In the example below, note the similarities and differences from the above example.
1. Like the example above, the less-than sign is color-coded to match the numbers that make the statement true.
This inequality statement represents all temperatures below 80 degrees.
2. The circle at the top of the number line is not filled in at 80.
This means that a temperature of 80 degrees is NOT included.
It also means that all temperature values below 80, will make the inequality statement true.
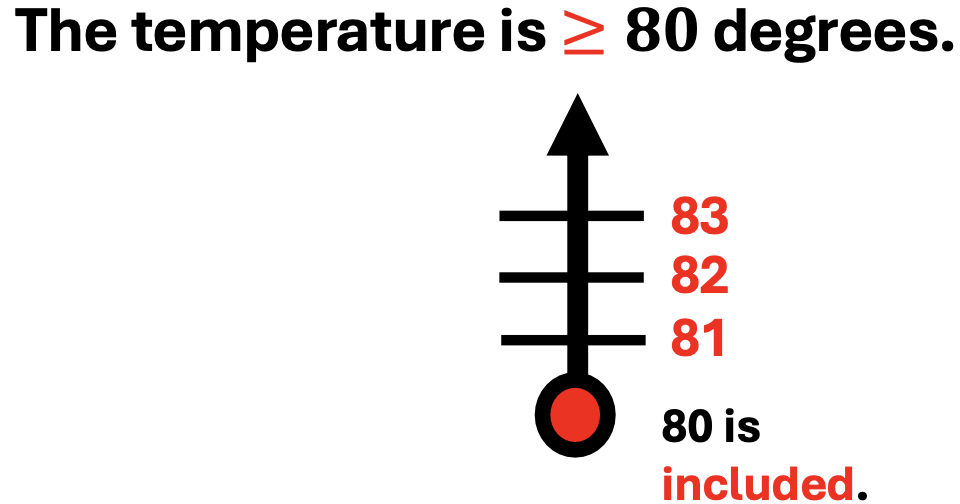
Next, ask students to make observations related to the similarities and variations with the use of the greater than or equal sign.
1. Like the greater-than sign in a previous example, the numbers are color-coded to represent all numbers greater than 80.
The line below the greater-than sign means that 80 is also included.
2. Finally, note that the circle is filled, meaning that 80 is also included as a solution of the statement.
Continue to ask for student observation.
The following example illustrates the less-than or equal sign. Like the greater-than or equal sign, the circle on the graph is filled, meaning 80, and all numbers less than 80 make the inequality statement true.
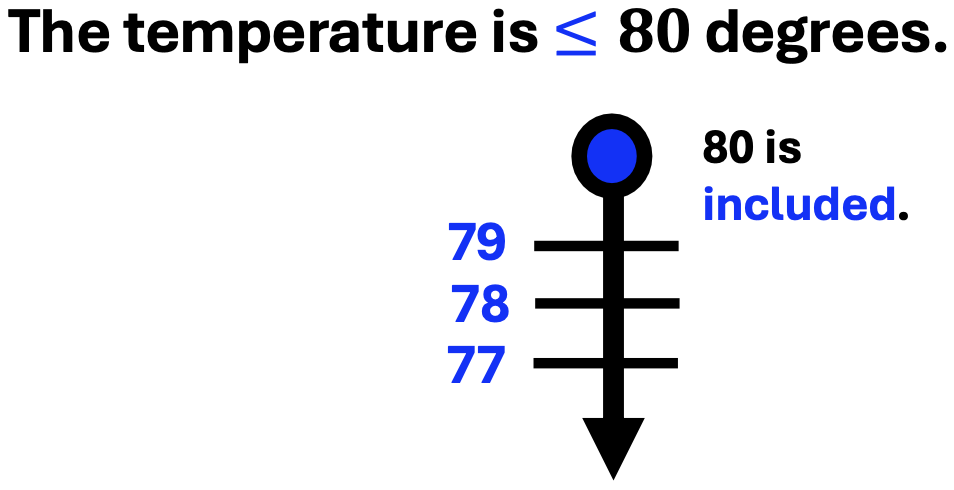
B. Examples of Horizontal Number Lines Using Money
Money is another great way to introduce your students to inequalities and number lines. Below is an example. Notice the following:
1. The greater-than sign is color-coded to match the numbers that make the statement true.
Juan has greater-than five dollars. This means that Juan could have 6, 7, 8, or even more dollars.
Notice that the amount of money Juan could have, continues to increase as the numbers continue to the right.
2. The circle of the number line is not filled.
This means that five is NOT included.
It also means that all number values greater than 5, will make the inequality statement true.
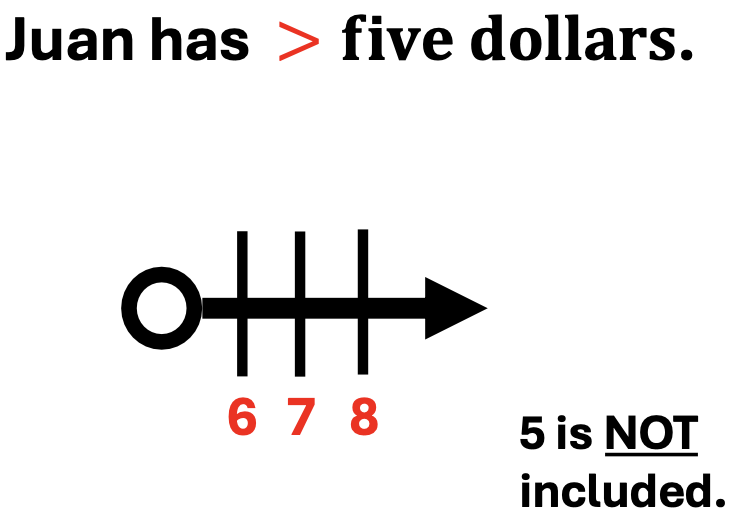
Students may question why 5 is not included, as they may reason,
“If I have 6 dollars, I must have 5 dollars, also.”
To help students understand this concept, emphasize that the reasoning is based on the inequality statement, “greater than” meaning that all numbers that make the statement true, must be greater than five.
For a visual, illustrate the following examples:
8 > 5: Is this a true statement? Yes.
5>5: Is this a true statement? No.
Though the number line is horizontal, continue to ask your class to make further observations.
In the next inequality statement, notice the following:
1. The less-than sign is also color-coded to match the numbers that make the statement true.
Juan has less than five dollars.
Notice that the amount of money Juan could have, decreases as the numbers continue to the left.
2. The circle at the bottom of the number line is not filled.
This means that five is NOT included.
It also means that all number values less than 5, will make the inequality statement true.
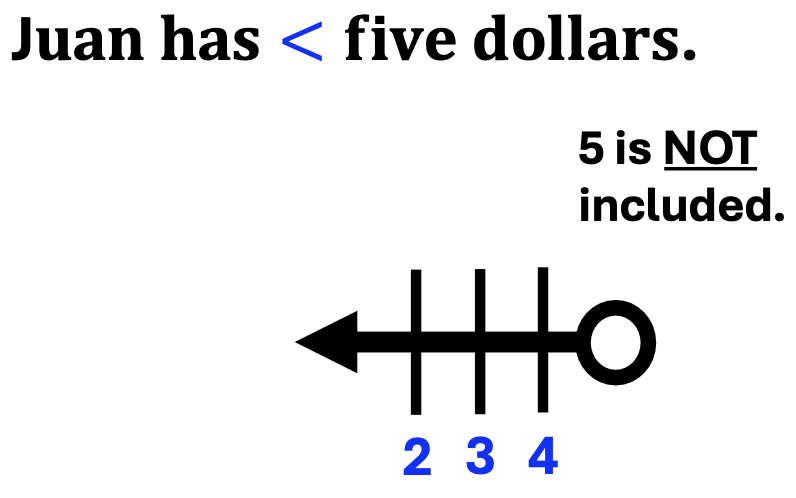
In the next inequality statement, notice the following:
1. The greater-than or equal sign is also color-coded to match the numbers that make the statement true.
Juan has five dollars or more. This means that Juan could have 5, 6, 7, or more dollars.
Notice that the amount of money Juan could have, continues to increase as the numbers continue to the right.
2. The circle of the number line is filled in.
This means that five IS included.
It also means that all number values five and greater than five will make the inequality statement true.
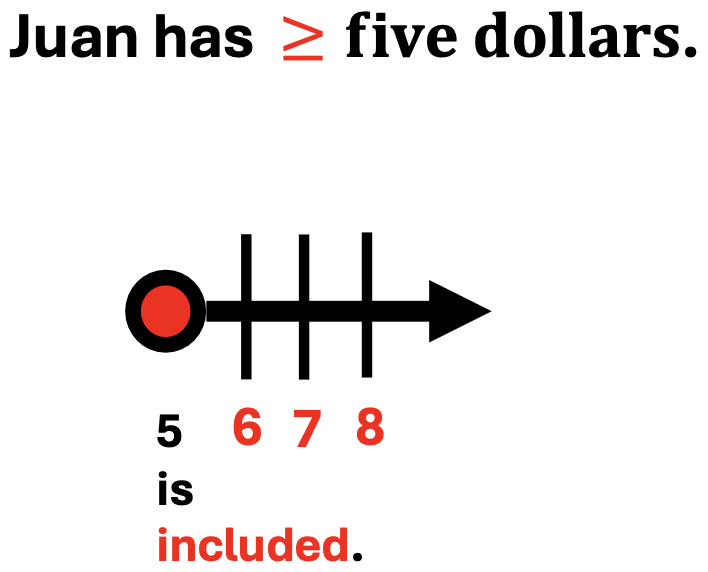
In the next inequality statement, notice the following:
1. The less-than or equal sign is also color-coded to match the numbers that make the statement true.
Juan has five dollars or less. Juan could have 5, 4, 3, or or less dollars.
Notice that the amount of money Juan could have, continues to decrease as the numbers continue to the left.
2. The circle at the bottom of the number line is filled in.
This means that five IS included.
It also means that all number values from five and less than five, will make the inequality statement true.
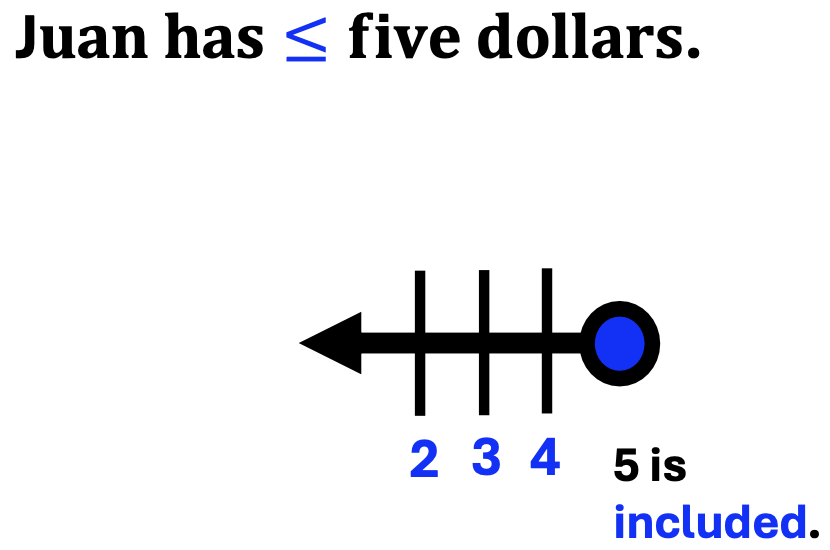
#3 – What to Do: To Fill or Not to Fill?
You may have students who forget when to leave a circle open or when to fill it. I respond to my students in the following visual way:



# 4 – Plan for a Poster Competition: Fun for All
You have taught the lesson, and could provide worksheets for practice. On the other hand, you could choose to assign an engaging activity that will require more processing and allow for creative thinking.
Ofcourse. Have students design their own posters to illustrate what they have just learned.
Materials Needed
Poster-size paper, scissors, rulers, glue, construction paper, markers, crayons, yarn, stickers, and other craft materials.
Prior to Beginning the Project
Students may list winning categories such as the most seasonal, colorful, artistic, interesting, entertaining, 3 dimensional, color-coordinated, etc.
Create Groups
It is ideal to have three to four persons to a group.
Objective
Each group is to design 4 posters that include inequality statements for less than, greater than, less than or equal to, and greater than. Each poster should represent a different sign. Encourage students to come up with an example that has not been discussed in class. For example, instead of using an illustration related to temperature or money, an illustration reflecting the rise and fall of the height of a river.
Each poster must also include an illustrated number line reflecting the inequality statement.
Conclusion
As you help students understand inequalities and number lines, the use of color, detailed examples, and applications to every-day life, and creative activities will increase student success with inequality problems.
Looking for More Materials?
Click the button below to view more of my educational resources!
