Are you looking for a way to easily explain exponents in a way that students will understand the first time? No problem. Keep scrolling to see strategies to help students understand exponents in Pre-Algebra.
#1 – Illustrate Examples Using Consistent Color-Coding
First, introduce students to exponents in pre-algebra by pointing out the parts and the names. Explain that the larger number is the base. Below you will notice that I color-coded the base value, blue. This is used to help students visualize the “base” associated with the color blue. I use the color, red for the exponent, and share with my students that the exit sign letters are red and add that the first two letters of the word, “exponent” also begin with the letters “ex“.

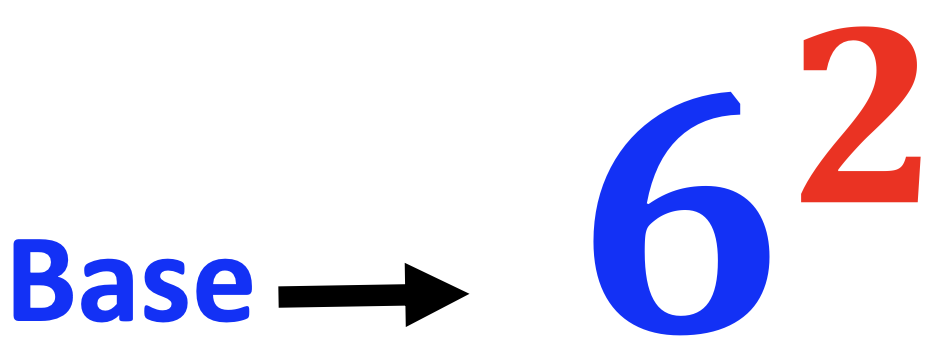

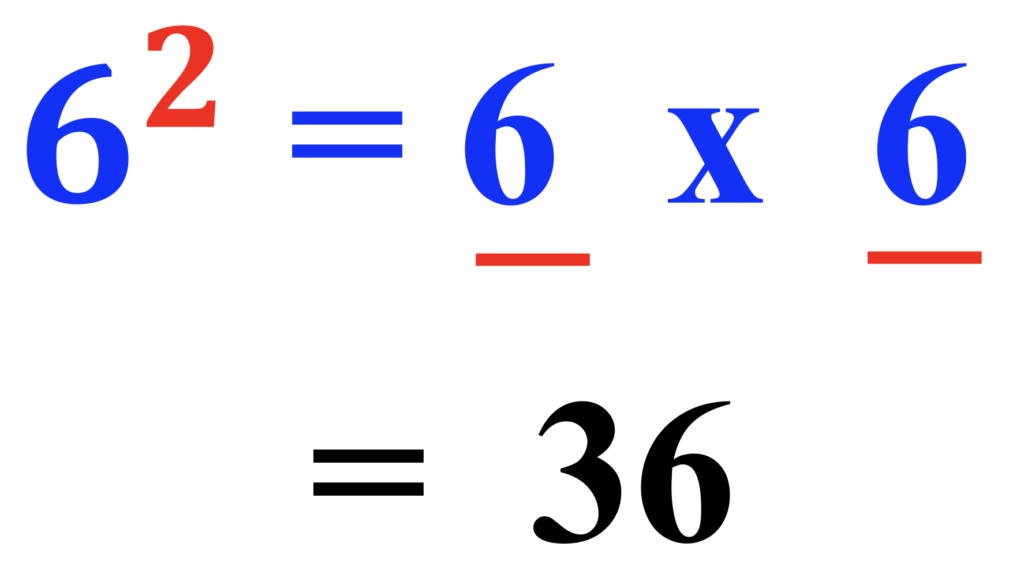
#2 – Strategies for Illustrating Exponents in Pre-Algebra
Second, continue using color to explain the meaning of the base with its exponent value.
You may have discovered that students’ most common assumption is that the base and the exponent are multiplied. For example, if the base is 9 and the exponent is 2, students may state that the answer is 18. To help students see more clearly, continue with color-coding and then ask students the following questions:
Q: “What is the base?”
A: “Nine”.
Q: “What is the exponent?”
A: “Two.”
Instruct:
“Two is the exponent. Draw two red lines with a multiplication sign in between the red lines.”
“Place the base of nine on each line.”
“Multiply”
“Nine squared is 81.”
See the example below.

Furthermore, a similar strategy can be provided for other numbers with exponents in Pre-Algebra math problems.
In the example below, the base is 7 and the exponent is 3.
Q: “What is the base?”
A: “Seven”.
Q: “What is the exponent?”
A: “Three.”
Instruct:
“Three is the exponent. Draw three red lines with a multiplication sign in between each red line.”
“Place the base of seven on each line.”
“Multiply”
“Seven cubed is 343.”

Encourage students to use this same method with blue and red pencils.
Below is a print-and-go product prepared for student practice saving you time.

#3 – Share the Special Rule for 0 and 1
Third, share that a base with an exponent of zero or one is special.
Prior, you may want to have fun with the exponents of zero and one. Here is how:
Give your students the number 1,279 with an exponent of zero. Ask students to determine the answer. You may also share,
“And by the way, the answer is not zero.”
Next, explain the special exponent of zero. Below is an illustration to help students visually associate the zero exponent resulting in the number, 1.
Point the zero exponent and spell the word, One = 1. Next, give several numbers that would represent the same answer.

Next, explain that any number with an exponent of one will be the same number. Said another way, the number representing the base, will be the answer for a number with an exponent of one.
The red line method could also be applied to a number with an exponent of 1. For example, 243 with an exponent of 1 would result in the base (243 written in blue) on only one red line.
Q: “What is the base?”
A: “Two-hundred forty-three”.
Q: “What is the exponent?”
A: “One.”
Instruct:
“One is the exponent. Draw one red line.”
“Place the base of two-hundred forty-three on the red line.”
“Two-hundred forty-three with an exponent of one is 243.”

#4 Memorize Numbers with Exponents of 4 and 5
Below are some of the most common exponent values in pre-algebra homework problems. Students will quickly recognize the solution for numbers with bases with zero and one, though other bases such as 2 – 5 may be less familiar. On the other hand, when students memorize the others, they will increase their ability to quickly solve order of operation problems that include exponents and roots.
Base Numbers 0 – 5 with an Exponent of 4
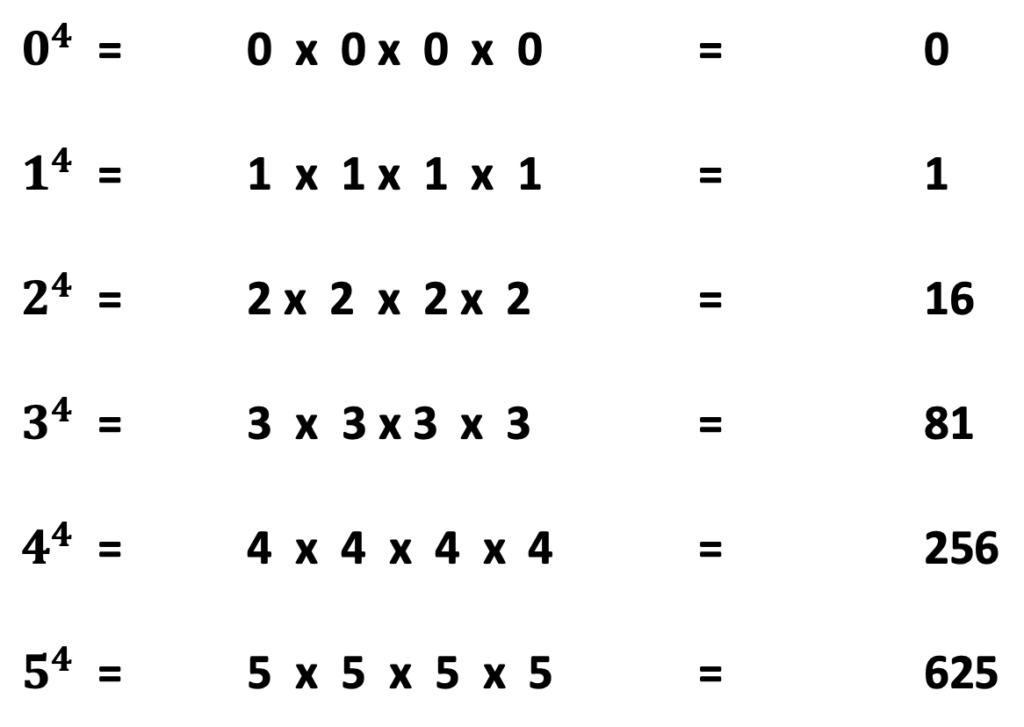
Base Numbers 0 – 5 with an Exponent of 5
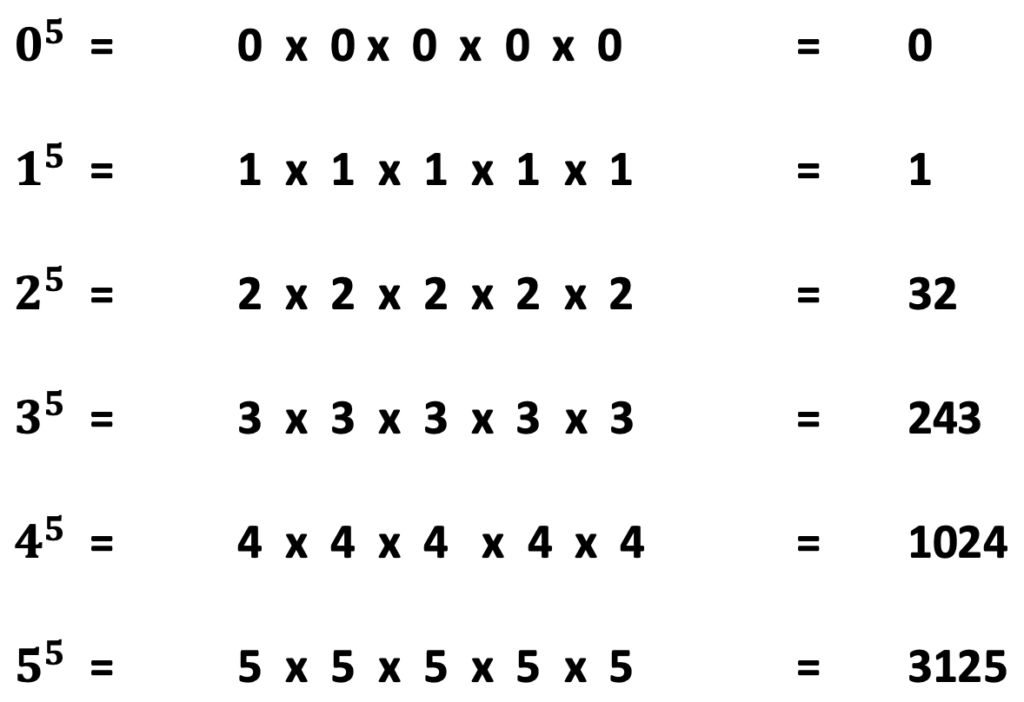
Conclusion
When using these strategies, students will easily understand the function of exponents as applied to positive number bases. Understanding these concepts will also provide the opportunity to complete order of operation problems that include exponents.
You may also be interested in the post, “Square and Cube Roots”. Just click on the title link below to learn more.
Looking for More Materials?
Click the button below to view more of my educational resources!
